ベクトルは向きと大きさをもった量を表します。
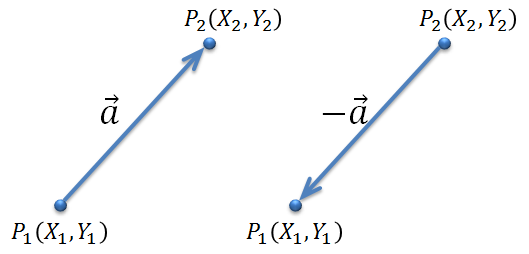
向きが逆の場合、ベクトルは負となります。
ベクトルを座標で表すと以下のようになります。
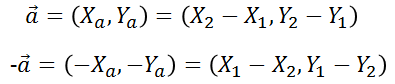
ベクトルの大きさは三平方の定理より、以下のようになり、この大きさをノルムと言います。
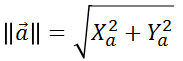
三次元の場合も同様に点P1(X1,Y1,Z1)から点P2(X2,Y2,Z2)へ向かうベクトルの場合は
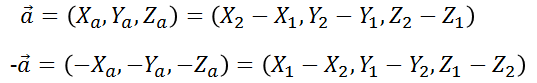
となり、ノルムも
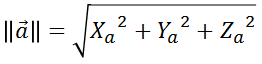
となります。
ここまでは、ベクトルを矢印で表す事のできるベクトルで幾何ベクトルと言います。
画像処理においては、より一般的にn個の数の組み合わせからなるn次元ベクトルとして扱う場合があります。
表記方法は一般に文字を太字にして
![]()
のように書きます。
こうなると、矢印で表す事ができなく、数ベクトルと言います。
画像処理的には、例えば、輝度値の平均、最小値、最大値、分散を使った
a=(平均、最小値、最大値、分散)
のような4次ベクトル!みたいな扱いをしたりします。(かなりいいかげんな例ですが。)
最初はなんでこんな難しそうに聞こえる(頭が良さそうに聞こえる)表現をするんだろうな~と思っていましたが、ベクトルとして扱う事で、内積などのベクトルの演算が使えたり、行列としても扱えたりするので、それなりのメリットも出てきます。

コメント