行列の基礎

正方行列

行と列の数が同じ行列

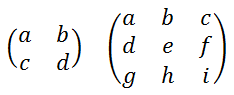
など

単位行列

行と列の位置が同じ場所の成分（対角成分）が１、それ以外が０となる行列

など。
EやIであらわされる。

AE=EA=A

が成り立つ。

零行列

全ての行列の成分が　０ となる行列

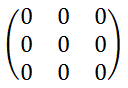
など。
O であらわされる。

転置行列

行と列の成分を入れ替えた行列を転置行列という。
行列Aの転置行列はTを使ってA^Tとあらわす。

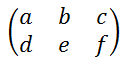
の転置行列は

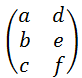
となる。

行列の足し算、引き算

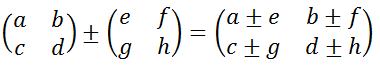
行列の積

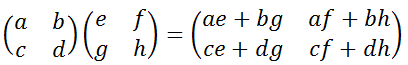
行列の計算

各行列A、B、Cにおいて

A + B = B + A
(A + B) + C = A + (B + C)
(AB)C = A(BC)
A(B + C) = AB + AC
(AB)^-1 = B^-1A^-1
(AB)^T = B^TA^T
(A^T)^T = A
(A^TB)^T = B^TA

が成り立ちます。

ただし、単位行列以外の計算では、行列の掛ける順番を入れ替えると、答えは異なります。

AB≠BA

←使える数学へ戻る