最小自乗法という人もいますが、私は最小二乗法派です。
最小二乗法とは?
点の集まりから、近似直線(曲線)などの近似式を解くための手法です。
単に直線や二次曲線、三次曲線などに限らず、最小二乗法の応用範囲は広くあります。
最小二乗法は、言葉の通りに2乗を最小にする方法なのですが、この2乗と言うのが、方程式上の理論値と近似するデータとの差の2乗の合計を最小にする方法となります。と言っても分かりづらいので、具体的な最小二乗法の例を示します。
最小二乗法の計算方法
今回は説明を簡単にするため、f(X)= aX + b の直線でデータを近似する場合で説明します。
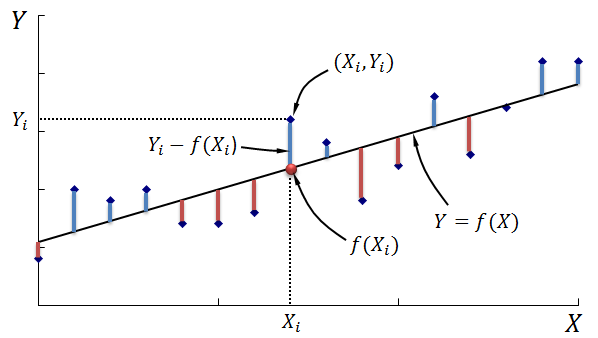
X = Xi のとき、直線上のY座標は
$$Y_{i}=f(X_{i})=aX_{i}+b$$
より、点と近似直線との差は
$$Y_{i}-f(X_{i})=Y_{i}-(aX_{i}+b)$$
となります。
この差の合計が一番小さい時にもっとも点の集まりを直線で近似できていることとなりますが、
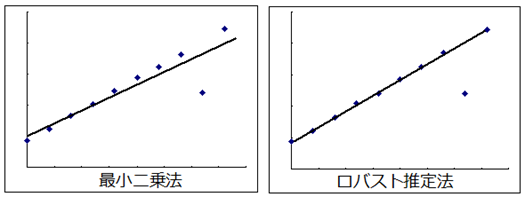
そのままこの差の総和を計算すると差の値がプラスの時とマイナスの時があるため、例えば下図
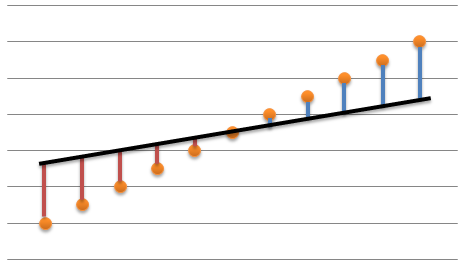
のように、正の差と負の差が同じようにある場合、差の合計が小さくなってしまうため、差を2乗してから合計した値が最小になるようにします。
よって、差の2乗の合計は
$$\sum(Y_{i}-(aX_{i}+b))^{2}\\
=\sum(a^{2}X_i^2+2aX_{i}b+b^{2}-2aX_{i}Y_{i}-2bY_{i}+Y_i^2 )$$
・・・式①
となり、この総和の値が最小となるaとbを求めれば近似直線を求められることとなります。
この式を良くみると、aとbの二次関数でできているため、この二次関数が最小となる値を求めればよい。
二次関数が最小となるのは微分した値 = 0 の場合であるから、式①をaとbで偏微分した値が
0(ゼロ)となる値を求めればよい。
式①をaとbでそれぞれ偏微分すると
$$\frac{\partial}{\partial a}=2a\sum X_i^2+2b\sum X_{i}-2\sum X_{i}Y_{i}=0\\
\frac{\partial}{\partial b}=2a\sum X_i+2b\sum 1-2\sum Y_{i}=0$$
より
$$a\sum X_i^2+b\sum X_{i}-\sum X_{i}Y_{i}=0\\
a\sum X_i+b\sum 1-\sum Y_{i}=0$$
となり、未知数がaとbで式が2本あることから、aとbの連立法的式を解くことで未知数a,bを求めることができます。
連立方程式を行列で表すと
$$\left(\begin{array}{c}\sum X_i^2 & \sum X_{i}\\ \sum X_{i} & \sum 1\end{array}\right)\left(\begin{array}{c}a\\ b\end{array}\right)=\left(\begin{array}{c}\sum X_{i}Y_{i}\\ \sum Y_{i}\end{array}\right)
\\
\left(\begin{array}{c}\sum X_i^2 & \sum X_{i}\\ \sum X_{i} & \sum 1\end{array}\right)^{-1}\left(\begin{array}{c}\sum X_i^2 & \sum X_{i}\\ \sum X_{i} & \sum 1\end{array}\right)\left(\begin{array}{c}a\\ b\end{array}\right)=\left(\begin{array}{c}\sum X_i^2 & \sum X_{i}\\ \sum X_{i} & \sum 1\end{array}\right)^{-1}\left(\begin{array}{c}\sum X_{i}Y_{i}\\ \sum Y_{i}\end{array}\right)
\\
\left(\begin{array}{c}a\\ b\end{array}\right)=\left(\begin{array}{c}\sum X_i^2 & \sum X_{i}\\ \sum X_{i} & \sum 1\end{array}\right)^{-1}\left(\begin{array}{c}\sum X_{i}Y_{i}\\ \sum Y_{i}\end{array}\right)
\\
\left(\begin{array}{c}a\\ b\end{array}\right)=\frac{1}{\sum X_i^2\sum 1-\sum X_{i}\sum X_{i}}\left(\begin{array}{c}\sum 1 & -\sum x_i\\ -\sum x_i & \sum X_i^2\end{array}\right)\left(\begin{array}{c}\sum X_iY_i\\ \sum Y_i\end{array}\right)$$
となり、行列を解くと未知数a,bが求まり、近似直線を求めることができます。
ちなみに、二次式(aX2 + bX + c)で近似すると
$$\left(\begin{array}{c}a\\ b \\ c\end{array}\right)=
\left(\begin{array}{c}
\sum X_i^4 & \sum X_i^3 & \sum X_i^2\\
\sum X_i^3 & \sum X_i^2 & \sum X_i\\
\sum X_i^2 & \sum X_i & \sum 1
\end{array}\right)^{-1}
\left(\begin{array}{c}
\sum X_i^2Y_i\\
\sum X_iY_i \\
\sum Y_i\end{array}\right)$$
三次式(aX3 + bX2 + cX + d)で近似すると
$$\left(\begin{array}{c}
a\\
b\\
c\\
d
\end{array}\right)=
\left(\begin{array}{c}
\sum X_i^6 & \sum X_i^5 & \sum X_i^4 & \sum X_i^3\\
\sum X_i^5 & \sum X_i^4 & \sum X_i^3 & \sum X_i^2\\
\sum X_i^4 & \sum X_i^3 & \sum X_i^2 & \sum X_i\\
\sum X_i^3 & \sum X_i^2 & \sum X_i & \sum 1
\end{array}\right)^{-1}
\left(\begin{array}{c}
\sum X_i^3Y_i\\
\sum X_i^2Y_i\\
\sum X_iY_i \\
\sum Y_i\end{array}\right)$$
と規則的に変化するため、n次式近似のプログラムも簡単に作ることができます。
ただし、行列の部分を二次元配列と考えると、近似する次数(n)が上がって行くと、配列の先頭に値が追加されていくのは、扱いにくいので、n次式近似のプログラムを作る場合は、近似式を
$$Y=a+bX+cX^2+dX^3 \cdot\cdot\cdot\cdot$$
として、行列の表現は
$$\left(\begin{array}{c}a\\ b\\ c\\d\\:
\end{array}\right)=
\left(\begin{array}{c}
\sum 1 & \sum X_i & \sum X_i^2 & \sum X_i^3 & .. \\
\sum X_i & \sum X_i^2 & \sum X_i^3 & \sum X_i^4 & .. \\
\sum X_i^2 & \sum X_i^3 & \sum X_i^4 & \sum X_i^5 & ..\\
\sum X_i^3 & \sum X_i^4 & \sum X_i^5 & \sum X_i^6 & ..\\
: & : & : & : & :
\end{array}\right)^{-1}
\left(\begin{array}{c}
\sum Y_i\\
\sum X_iY_i \\
\sum X_i^2Y_i\\
\sum X_i^3Y_i\\
:
\end{array}\right)$$
として、n次式で近似した最小二乗法を求めます。
この計算をエクセルで行ったものはExcelによる最小二乗近似からダウンロードできます。
逆行列を求めるプログラムにはガウスの消去法などが用いられます。
最小二乗法での注意点
三次式(a+bX+cX2+dX3)の近似を例にとってみると、近似処理をする過程でXに関する計算式はX~X6まで計算されます。
ここで、例えばXの値の範囲が
0.01~1000
だったとすると、Xに関する計算では
0.000000000001~1000000000000000000
までの計算がされます。
逆行列の計算ではこれらの値に関して足し算や掛け算がなされる訳ですからコンピュータの
計算誤差(桁落ち、情報落ちなど?)が発生する場合があります。
これを防ぐために、最小二乗法のプログラムでは近似式をそのまま使うのではなく、Xの値から
Xの平均値(Xb)を引いた計算式
$$Y=a+b(X-X_b)+c(X-X_b)^2+d(X-X_b)^3$$
で処理を行うのが一般的です。
最小二乗法の関連記事
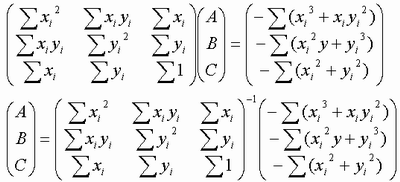
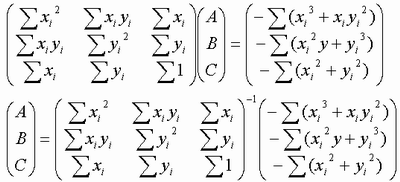


コメント
「となり、行列を解くと未知数a,bが求まり、近似直線を求めることができます。」
の上の図の最後の行の-1は不要ではないでしょうか?
ご指摘ありがとうございます。
おっしゃる通り、間違ってました。
記事も修正しました。
[…] 6/2 最小二乗法 […]
[…] 6/2 最小二乗法 […]