シグモイド関数の微分の計算方法

シグモイド関数を微分するには合成関数の微分を用いて行います。

まず、シグモイド関数

$$f(x)=\frac { 1 }{ 1+{ e }^{ -x } } $$

において

$$u=g(x)=1+{ e }^{ -x }$$

と置くと、

$$y=f(u)=\frac { 1 }{ u } ={ u }^{ -1 }$$

より、合成関数の微分を使って

$$f'(x)=\frac { dy }{ dx } =\frac { dy }{ du } \frac { du }{ dx } \\ =-{ u }^{ -2 }(-{ e }^{ -x })\\ =\frac { { e }^{ -x } }{ { u }^{ 2 } } \\ =\frac { { e }^{ -x } }{ (1+{ e }^{ -x }) ^{ 2 }}$$

となりますが、この先がちょとトリッキーな式の変形を行い、

$$=\frac { { e }^{ -x } }{ 1+{ e }^{ -x } } \frac { 1 }{ 1+{ e }^{ -x } } \\ =(\frac { { 1+e }^{ -x } }{ 1+{ e }^{ -x } } -\frac { 1 }{ 1+{ e }^{ -x } } )\frac { 1 }{ 1+{ e }^{ -x } } \\ =(1-\frac { 1 }{ 1+{ e }^{ -x } } )\frac { 1 }{ 1+{ e }^{ -x } }$$

となります。

ここで

$$f(x)=\frac { 1 }{ 1+{ e }^{ -x } } $$

であるから、

$$f’(x)=(1-f(x))f(x)$$

となるのが、シグモイド関数の微分となります。

例によってPythonのmatplotlibを使ってグラフを書いてみると、

import matplotlib.pyplot as plt
import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.linspace(-10, 10)

#シグモイド関数
y = sigmoid(x)
plt.plot(x, y)

#シグモイド関数の微分
dy = (1 - sigmoid(x)) * sigmoid(x)
plt.plot(x, dy)

plt.show()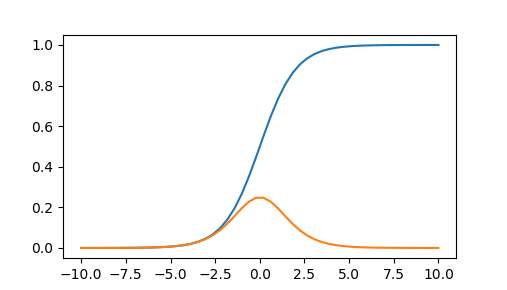

途中の計算は、自分一人では解けないな。。きっと。