OpenCVには座標を楕円で近似する関数(fitEllipse)はあるものの、円で近似するfitCircle()のような関数はありません。
そこで、最小二乗法的に座標を円で近似するfitCircle()関数を作ってみました。
円の最小二乗法については、以前、書きました。
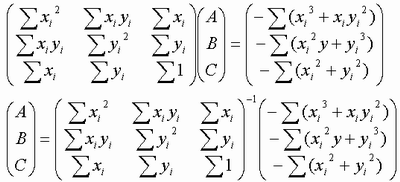
この記事で行っている最小二乗法はベタに式を2乗して、未知数で偏微分する必要があるので、計算が少々面倒です。
そこで、今回は、疑似逆行列を使って円近似を行いたいと思います。
疑似逆行列を用いた円近似
円上の座標を(x, y)、円の中心座標を(a, b)、半径を r とすると、円の公式は
$$(x-a)^{2}+(y-b)^{2}=r^{2}$$
この式を展開すると
$$x^{2}-2ax+a^{2}+y^{2}-2by+b^{2}=r^{2}$$
となります。
ここで、
$$\begin{cases}A = -2a\\B = -2b\\C = a^{2}+b^{2}-r^{2}\end{cases}$$
と置き、式を整理すると、
$$Ax+By+C=-x^{2}-y^{2}$$
となります。
近似に用いる点の座標を \((x_{1},y_{1}), (x_{2},y_{2}), (x_{3},y_{3})・・・\)とすると
$$\begin{cases}Ax_{1}+By_{1}+C=-x_{1}^{2}-y_{1}^{2}\\Ax_{2}+By_{2}+C=-x_{2}^{2}-y_{2}^{2}\\Ax_{3}+By_{3}+C=-x_{3}^{2}-y_{3}^{2}\\ :\end{cases}$$
のように、近似する座標の点数(円近似の場合は3点以上必要)ぶんだけの式が成り立ちます。
この連立方程式を行列で表すと、
$$\left(\begin{array}{c}x_{1}&y_{1}&1\\ x_{2}&y_{2}&1\\x_{3}&y_{3}&1\\ &:\end{array}\right)\left(\begin{array}{c}A\\ B\\C\end{array}\right)=\left(\begin{array}{c}-x_{1}^{2}-y_{1}^{2}\\ -x_{2}^{2}-y_{2}^{2}\\ -x_{3}^{2}-y_{3}^{2}\\ :\end{array}\right)$$
となるので、あとは疑似逆行列を使えば、A, B, C が求まるので、A, B, Cの値から円の中心座標の(a, b)、半径の r が求まります。
$$\begin{cases}a=-\frac{A}{2}\\b=-\frac{B}{2}\\r=\sqrt{a^{2}+b^{2}-C}\end{cases}$$
疑似逆行列を求める部分についはnumpyにlinalg.pinvという関数があるので、これを用います。
サンプルプログラム
上記の疑似逆行列を用いた円近似の処理をまとめました。
円近似の fitCircle()関数を作成しています。
import cv2
import numpy as np
def fitCircle(contour):
'''
座標の円近似(最小二乗円)
'''
matA = []
matB = []
for point in contour:
x = point[0,0]
y = point[0,1]
matA.append([x,y,1])
matB.append([-x*x -y*y])
# listからndarrayへ変換
matA = np.array(matA, np.float32)
matB = np.array(matB, np.float32)
# 疑似逆行列を求める
matA_pinv = np.linalg.pinv(matA)
# 行列の解
matX = matA_pinv.dot(matB)
# 中心座標
a = -matX[0,0]/2
b = -matX[1,0]/2
# 半径
r = np.sqrt(a*a+b*b-matX[2,0])
# 中心座標, 半径
return (a, b), r
##########################################################################
# 8ビット1チャンネルのグレースケールとして画像を読み込む
img = cv2.imread("image.jpg", cv2.IMREAD_GRAYSCALE)
# 白黒反転して二値化
ret, img = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY_INV)
# 一番外側の輪郭のみを取得
contours, hierarchy = cv2.findContours(img, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_NONE )
# 画像表示用に入力画像をカラーデータに変換する
img_disp = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)
# 全ての輪郭を描画
cv2.drawContours(img_disp, contours, -1, (0, 0, 255), 2)
# 輪郭の点の描画
for contour in contours:
# 円近似
center, r = fitCircle(contour)
# 近似円を描画
cv2.circle(img_disp, np.intp(center), int(r), (255, 0, 0), 2)
cv2.imshow("Image", img_disp)
# キー入力待ち(ここで画像が表示される)
cv2.waitKey()実行結果
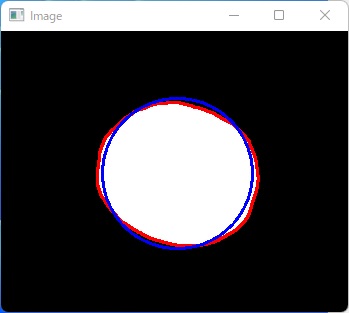
関連記事




コメント
このコードを応用して、斜め上から撮影したメーターの画像を正面から撮影したように補正することは可能でしょうか?
斜め上から撮影すると、四角形の画像を撮影した場合は、台形に映ります。
この台形を四角形にする変換は射影変換といいます。
射影変換は、OepnCVでは、findHomography(),warpPerspective()の関数を使いますが、私の記事の中では書いていませんでした。。
Pillowを使った例で良ければ、こちら↓を参考にしてください
https://imagingsolution.net/program/python/pillow/pillow_transform_quad/