一般的に明るさは距離の2乗に反比例すると言われます。
なぜか???
光源のある点から放たれた光は放射線状に広がり、点から距離が同じ位置では明るさが等しくなります。
点から同じ位置という事は、点を中心とした球面上の明るさは等しくなります。
さらに、この球面上の明るさを全て足し合わせると、全ての光量は、どの距離でも等しくなります。
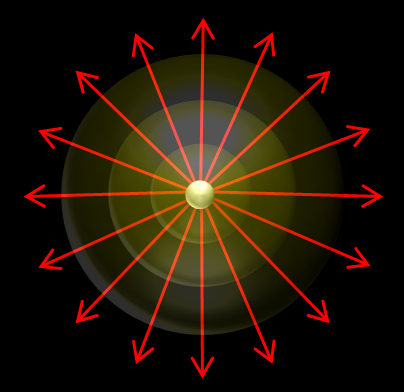
つまり、明るさは球面の面積に反比例するので、球の表面積 4πr2 より、
明るさは距離の2乗に反比例する
という事になります。
でも、距離が遠くても、レンズで集光すれば、明るさは明るくなるのに?!って、ひねくれ者の私はすぐに思ってしまいます。
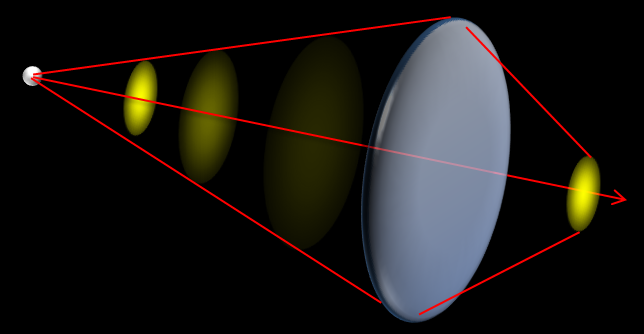
なので、ざっくりとは
明るさは面積に反比例する
と覚えておくと、大体合ってます。
”大体”というのは、面積が球面上の面積であればいいのですが、平面上の面積だと、平面上の明るさは距離が短いほど均一ではなく、レンズで集光する場合にも光量のロスがあるので、厳密な意味では無いのですが、マシンビジョンにおける照明の考え方としては、明るさは面積に反比例すると思っておくと十分な場合が多いです。(ちょっと荒っぽく、現場的な感覚ですが...)
最初に、光源のある点から放たれた光は・・・と言いましたが、光源が点で出来ている訳ではなく、ある程度の面積を持ちますよね?
その場合の考え方としては、例えば豆電球のような場合では、フィラメント上の各点から光るので、点の集まりとして捉えます。
この明るさは面積に反比例するという感覚を用いると、昔、理科の実験でやった顕微鏡の理屈もなんとなく説明できます。
倍率が低い場合は、平面鏡を用いて観察し、倍率が高い場合は凹面鏡を用いるように教わりました。
【倍率が低い場合】
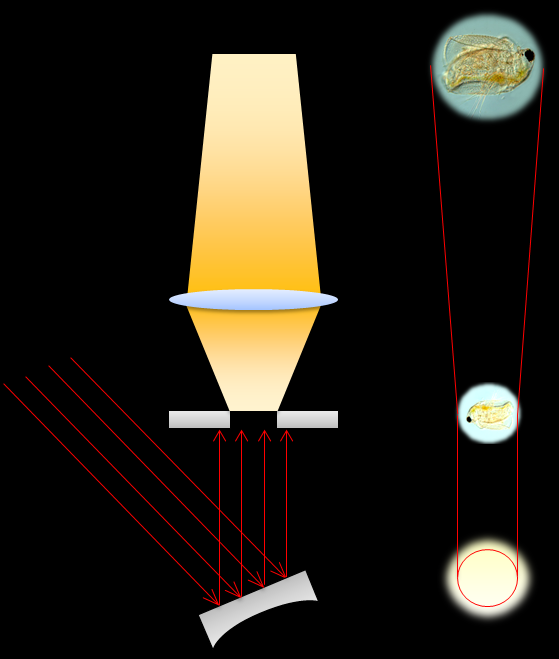
【倍率が高い場合】
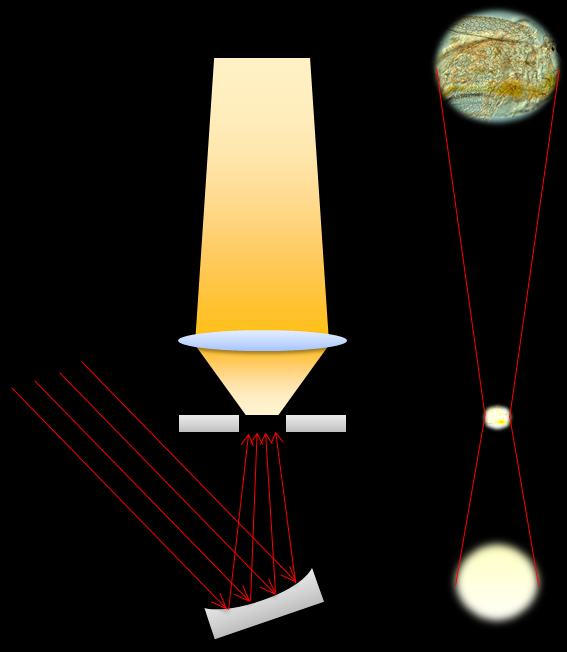
上図を見ると分かるように低倍率の場合は、被写体の位置の面積は、あまり拡大されず、高倍率の場合は被写体の位置の面積が大きく拡大されるので、より多くの光量が必要となります。
そこで、高倍率の場合は凹面鏡を用いて集光し(面積を小さくし)、被写体の位置での明るさを稼いでから、拡大する事で、光量不足を補っています。
と、いい大人になってから思う。
小学生の頃はそれ以前に、なんでこんなに明るい場所(教室)で見てるのに、そんなに明るくする必要があるんだろう???って思ってました。


コメント