アフィン変換では長方形を平行四辺形には変換できるものの、台形には変換できないと説明しましたが、任意四角形から任意四角形へ変換できるのがホモグラフィ変換となります。
実際には書類や名刺のような長方形の被写体を斜めから撮影した時に、上から撮影したような感じに長方形に見えるように変換するときにホモグラフィ変換が用いられることが多いです。


このホモグラフィ変換は、変換前の座標を(x, y)、変換後の座標を (x’, y’) とすると、
$$s\left(\begin{array}{c}x^{‘}\\ y^{‘}\\ 1\end{array}\right)
=
\left(\begin{array}{c}a & b & c\\ d & e & f\\ g & h & 1\end{array}\right)
\left(\begin{array}{c}x\\ y \\ 1\end{array}\right)$$
となります。
アフィン変換の行列と比較すると、変換後の座標の頭に s が付いているのと、アフィン変換行列の3行目の要素が 0 だった部分に g と h が登場しています。
このホモグラフィ変換の行列の計算は以下のようにします。
$$s\left(\begin{array}{c}x^{‘}\\ y^{‘}\\ 1\end{array}\right)
=
\left(\begin{array}{c}a & b & c\\ d & e & f\\ g & h & 1\end{array}\right)
\left(\begin{array}{c}x\\ y \\ 1\end{array}\right)$$
を展開し、
$$\begin{cases}sx^{‘}=ax+by+c\\sy^{‘}=dx+ey+f\\s=gx+hy+1\end{cases}$$
より
$$\begin{cases}x^{‘}=\frac{ax+by+c}{gx+hy+1}\\y^{‘}=\frac{dx+ey+f}{gx+hy+1}\end{cases}$$
となり、ホモグラフィ変換後の座標を求める事ができます。
式を見ると分かりますが、 g = h = 0 のときは s = 1 となり、アフィン変換そのものとなります。
つまり、アフィン変換で出来る変換はホモグラフィ変換でも可能です。
このホモグラフィ変換行列の未知数(a ~ h)を求めるには、座標からアフィン変換行列を求める方法でも似たような説明をしていますが、ホモグラフィ変換行列では未知数が8個なので8本の連立方程式を立てれば未知数を解く事ができます。
$$\begin{cases}x^{‘}=\frac{ax+by+c}{gx+hy+1}\\y^{‘}=\frac{dx+ey+f}{gx+hy+1}\end{cases}$$
の式を変形して、
$$\begin{cases}x^{‘}(gx+hy+1)=ax+by+c\\y^{‘}(gx+hy+1)=dx+ey+f\end{cases}$$
$$\begin{cases}ax+by+c-gxx^{‘}-hyx^{‘}=x^{‘}\\
dx+ey+f-gxy^{‘}-hyy^{‘}= y^{‘}\end{cases}$$
となり、この x, y, x’, y’ に変換前の座標 (x0, y0), (x1, y1), (x2, y2), (x3, y3)と変換後の座標
(x’0, y’0), (x’1, y’1), (x’2, y’2), (x’3, y’3)を代入すると、式が8本立つので、8個の未知数を求める事ができます。
実際に変換前、変換後の座標を代入して8本の式を書くと
$$\begin{cases}
ax_{0}+by_{0}+c-gx_{0}x_0^{‘}-hy_{0}x_0^{‘}=x_0^{‘}
\\
dx_{0}+ey_{0}+f-gx_{0}y_0^{‘}-hy_{0}y_0^{‘}= y_0^{‘}
\\
ax_{1}+by_{1}+c-gx_{1}x_1^{‘}-hy_{1}x_1^{‘}=x_1^{‘}
\\
dx_{1}+ey_{1}+f-gx_{1}y_1^{‘}-hy_{1}y_1^{‘}= y_1^{‘}
\\
ax_{2}+by_{2}+c-gx_{2}x_2^{‘}-hy_{2}x_2^{‘}=x_2^{‘}
\\
dx_{2}+ey_{2}+f-gx_{2}y_2^{‘}-hy_{2}y_2^{‘}= y_2^{‘}
\\
ax_{3}+by_{3}+c-gx_{3}x_3^{‘}-hy_{3}x_3^{‘}=x_3^{‘}
\\
dx_{3}+ey_{3}+f-gx_{3}y_3^{‘}-hy_{3}y_3^{‘}= y_3^{‘}
\end{cases}$$
となります。
この8本の式を行列を使って解くのですが、行列を使って連立方程式を解く時のポイントですが、未知数の部分を1列の行列になるようにして、行列で表現します。
今回の場合は、未知数が a~h までの8個あるので、
$$\left(\begin{array}{c}{}\\ {}\\ {}\\ {}&{}&{?}&{}&{}\\ {}\\ {}\\ {}\\ {}\end{array}\right)
\left(\begin{array}{c}a\\ b\\ c\\ d\\ e\\ f\\ g\\ h\end{array}\right)
=
\left(\begin{array}{c}{}\\ {}\\ {}\\ {?}\\ {}\\ {}\\ {}\\ {}\end{array}\right)$$
という形になるように連立方程式を行列で表現します。
すると、
$$\left(\begin{array}{c}
x_{0}&y_{0}&1&0&0&0&-x_{0}x_0^{‘}&-y_{0}x_0^{‘}
\\
0&0&0&x_{0}&y_{0}&1&-x_{0}y_0^{‘}&-y_{0}y_0^{‘}
\\
x_{1}&y_{1}&1&0&0&0&-x_{1}x_1^{‘}&-y_{1}x_1^{‘}
\\
0&0&0&x_{1}&y_{1}&1&-x_{1}y_1^{‘}&-y_{1}y_1^{‘}
\\
x_{2}&y_{2}&1&0&0&0&-x_{2}x_2^{‘}&-y_{2}x_2^{‘}
\\
0&0&0&x_{2}&y_{2}&1&-x_{2}y_2^{‘}&-y_{2}y_2^{‘}
\\
x_{3}&y_{3}&1&0&0&0&-x_{3}x_3^{‘}&-y_{3}x_3^{‘}
\\
0&0&0&x_{3}&y_{3}&1&-x_{3}y_3^{‘}&-y_{3}y_3^{‘}
\end{array}\right)
\left(\begin{array}{c}a\\ b\\ c\\ d\\ e\\ f\\ g\\ h\end{array}\right)
=
\left(\begin{array}{c}x_0^{‘}\\ y_0^{‘}\\ x_1^{‘}\\ y_1^{‘}\\ x_2^{‘}\\ y_2^{‘}\\ x_3^{‘}\\ y_3^{‘}\end{array}\right)$$
となるので、あとは逆行列を使って
$$\left(\begin{array}{c}a\\ b\\ c\\ d\\ e\\ f\\ g\\ h\end{array}\right)
=
\left(\begin{array}{c}
x_{0}&y_{0}&1&0&0&0&-x_{0}x_0^{‘}&-y_{0}x_0^{‘}
\\
0&0&0&x_{0}&y_{0}&1&-x_{0}y_0^{‘}&-y_{0}y_0^{‘}
\\
x_{1}&y_{1}&1&0&0&0&-x_{1}x_1^{‘}&-y_{1}x_1^{‘}
\\
0&0&0&x_{1}&y_{1}&1&-x_{1}y_1^{‘}&-y_{1}y_1^{‘}
\\
x_{2}&y_{2}&1&0&0&0&-x_{2}x_2^{‘}&-y_{2}x_2^{‘}
\\
0&0&0&x_{2}&y_{2}&1&-x_{2}y_2^{‘}&-y_{2}y_2^{‘}
\\
x_{3}&y_{3}&1&0&0&0&-x_{3}x_3^{‘}&-y_{3}x_3^{‘}
\\
0&0&0&x_{3}&y_{3}&1&-x_{3}y_3^{‘}&-y_{3}y_3^{‘}
\end{array}\right)^{-1}
\left(\begin{array}{c}x_0^{‘}\\ y_0^{‘}\\ x_1^{‘}\\ y_1^{‘}\\ x_2^{‘}\\ y_2^{‘}\\ x_3^{‘}\\ y_3^{‘}\end{array}\right)$$
を求めると未知数が求まるので、ホモグラフィ変換行列も求まります。
それでは、具体的に変換前、変換後の座標を使ってPythonのNumPyでホモグラフィ変換行列を解いてみたいと思います。
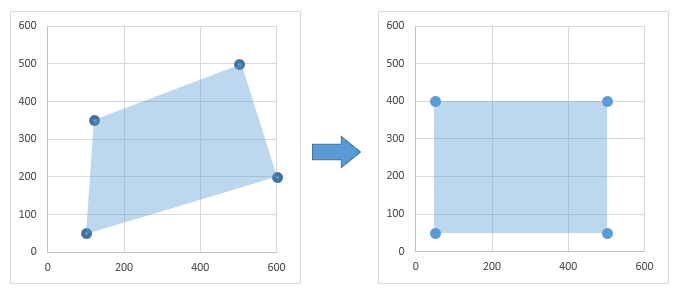
変換前 → 変換後
(100, 50) → (50, 50)
(120, 350) → (50, 400)
(500, 500) → (500, 400)
(600, 200) → (500, 50)
import numpy as np
mat = np.array([[100, 50, 1, 0, 0, 0, -100*50, -50*50],
[0, 0, 0, 100, 50, 1, -100*50, -50*50],
[120, 350, 1, 0, 0, 0, -120*50, -350*50],
[0, 0, 0, 120, 350, 1, -120*400, -350*400],
[500, 500, 1, 0, 0, 0, -500*500, -500*500],
[0, 0, 0, 500, 500, 1, -500*400, -500*400],
[600, 200, 1, 0, 0, 0, -600*500, -200*500],
[0, 0, 0, 600, 200, 1, -600*50, -200*50]])
dst = np.array([50, 50, 50, 400, 500, 400, 500, 50]).T
ans = np.matmul(np.linalg.inv(mat), dst)
homography = np.array([[ans[0], ans[1], ans[2]],
[ans[3], ans[4], ans[5]],
[ans[6], ans[7], 1]])
print(homography)
# 座標変換の確認
dst = np.matmul(homography, np.array([100, 50, 1]).T)
print("x'=", dst[0]/dst[2])
print("y'=", dst[1]/dst[2])
dst = np.matmul(homography, np.array([120, 350, 1]).T)
print("x'=", dst[0]/dst[2])
print("y'=", dst[1]/dst[2])
dst = np.matmul(homography, np.array([500, 500, 1]).T)
print("x'=", dst[0]/dst[2])
print("y'=", dst[1]/dst[2])
dst = np.matmul(homography, np.array([600, 200, 1]).T)
print("x'=", dst[0]/dst[2])
print("y'=", dst[1]/dst[2])(実行結果)
[[ 1.11407581e+00 -1.11269833e-01 -5.49716851e+01]
[-2.55930820e-01 9.08099927e-01 3.10604901e+01]
[ 5.63236570e-04 -7.77511351e-04 1.00000000e+00]]
x'= 50.000000000000064
y'= 50.000000000000014
x'= 50.000000000000135
y'= 400.00000000000006
x'= 500.0000000000006
y'= 400.0000000000002
x'= 500.00000000000057
y'= 50.000000000000064出来た!!
参考
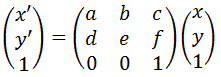




コメント