 Kinect
Kinect 【参考書籍】KINECT for Windows SDK プログラミング C#編
2012年2月の初旬に公開されたKinect for WindowsのSDKですが、もうすでにこのSDKの書籍が発刊されました。著者はKinect + OpenNIの本(KINECTセンサープログラミング)を書いた中村薫さんほか。仕事が早い...
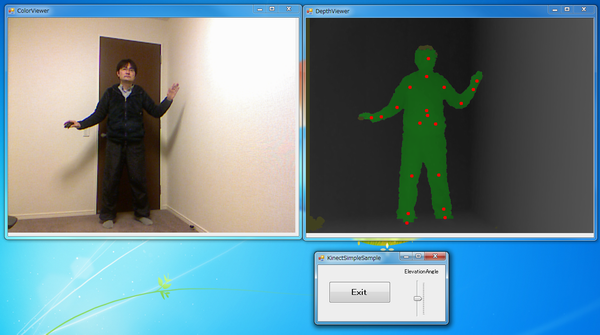 Kinect
Kinect 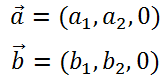 使える数学
使える数学 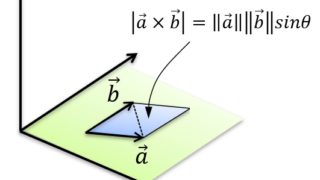 使える数学
使える数学 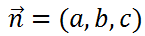 使える数学
使える数学 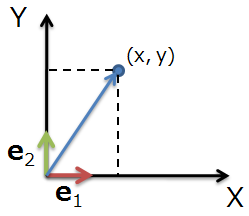 使える数学
使える数学 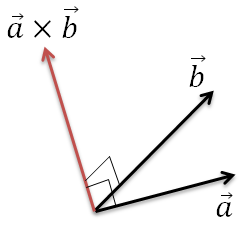 使える数学
使える数学  Excel
Excel 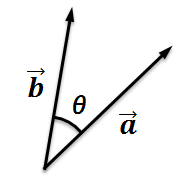 使える数学
使える数学 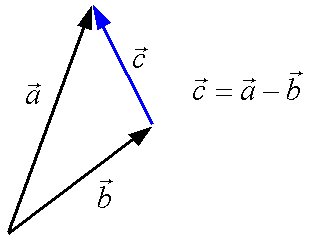 使える数学
使える数学 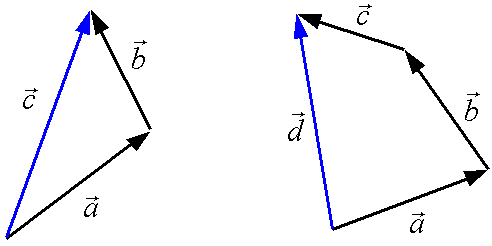 使える数学
使える数学 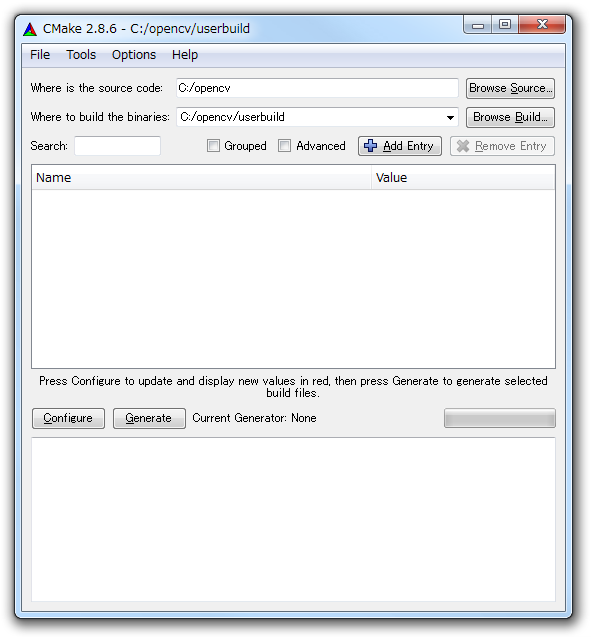 OpenCV
OpenCV 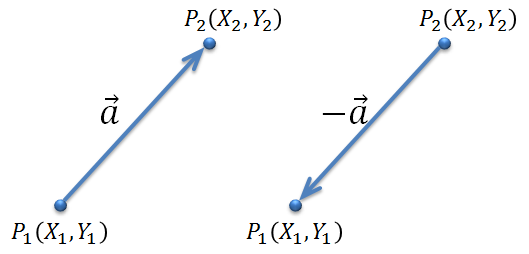 使える数学
使える数学 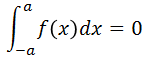 使える数学
使える数学  C#
C#