画像を拡大や回転する場合など、画像の画素と画素の間の輝度値を参照する必要が出てきますが、その参照方法を紹介します。
この画素を画素の間を参照する事を一般に補間や内挿(Interpolation)と言います。
最近傍補間(ニアレストネイバー Nearest neighbor)
Nearest neighborをそのまま訳すと、最も近いご近所、という事で参照する位置に最も近い位置にある画素の輝度値を参照します。
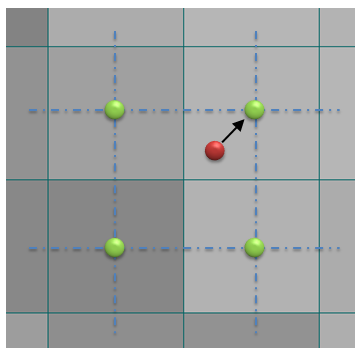
求める画素間の座標が(x,y)の位置の輝度値を Dst(x,y) とし、もともとの画像の輝度値をSrc(i,j) とすると
![]()
で表されます。(ただし、[ ] は小数部分の切り捨てを表します。)
つまるとこ、座標を四捨五入し、その画素の輝度値を参照します。
双一次補間(バイリニア補間 Bilinear)
バイリニア補間では求める位置(x,y)の周辺の2×2画素(4画素)を使って、輝度値を直線的に補間して、輝度値を求めます。
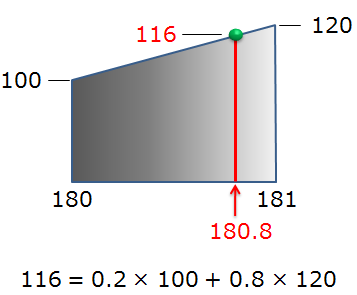
直線的に補間する方法は、たとえば下図のようにX座標が180と181の2点間の180.8の位置の輝度値を求めるのは、2点の位置の輝度値の比から簡単に求まります。
この処理を手前の2点間、奥の2点間についてX軸方向に補間処理を行い、さらに補間した2点の輝度値を用いて、さらにY軸方向に補間処理することで、目的の輝度値を求めます。
(Y軸方向から先に処理を行っても結果は同じです。)
ちなみに、このBilinearの接頭語のbi-ですが、『二つの、双方向』というような意味があるそうです。
ということで、双方向からリニア(直線的)に補間したのが、このBilinearで、次に出てくるBicubicは双方向から三次関数で補間したのが、Bicubicです。
この補間処理を式で表すと、
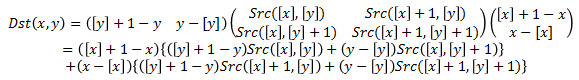
となります。
双三次補間(バイキュビック補間 Bicubic)
バイキュービック補間では求める位置(x,y)の周辺の4×4画素(16画素)を使って、輝度値を三次式で補間して輝度値を求めます。
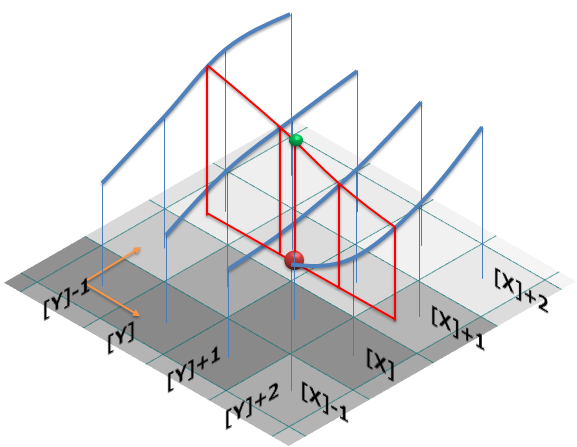
この変換を式で書くと
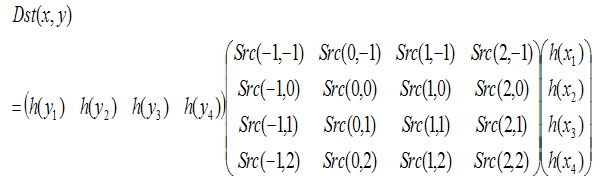
となります。
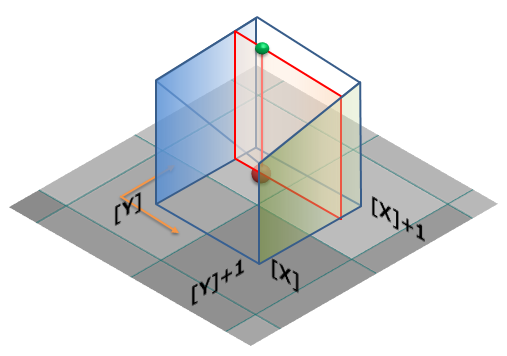
ただし、Src(i,j)は求める座標(x,y)の周辺の輝度値を表し、下図のような配置とします。
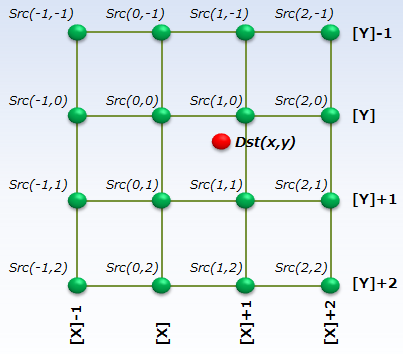
また、X1、X2、X3、X4、Y1、Y2、Y3、Y4 は求める位置から参照する画素までの距離を表し、
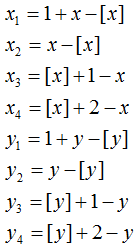
と定義します。
関数h(t)はsinc関数(sinc(t) = sin(πt)/πt) をテイラー展開により三次の項まで近似した関数で
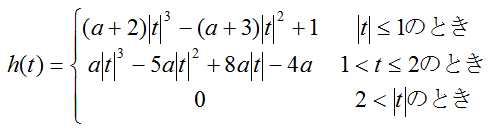
だそうで...(詳細は良く分かってません。)
a の値には-1前後がよく用いられます。
まとめ
各補間方法を使って、画像を拡大表示すると以下のようになります。
【元の画像】

赤い四角の部分を拡大表示します。
【Nearest neighbor】

【Bilinear】

【Bicubic】

これらの画像を見ても分かるようにNearest neighbor⇒Bilinear⇒Bicubicの順でギザギザなのがなめらかに拡大表示されます。
この変換を1次元的に輝度値のグラフで見てみると
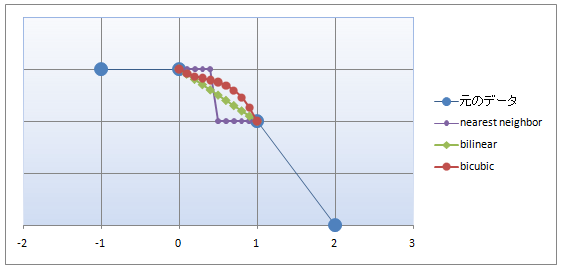
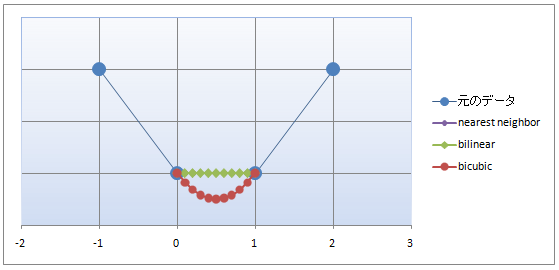

となります。
ここで注意しないといけないのが、Bicubic補間がおおむね滑らかに輝度値を補間することが
できますが、最後のグラフを見ても分かるように、輝度値がオーバーシュート(アンダーシュート)ぎみ
になる場合があります。その場合は補間の式の a の値を -0.2 程度のより0に近い値に
すると回避することができます。

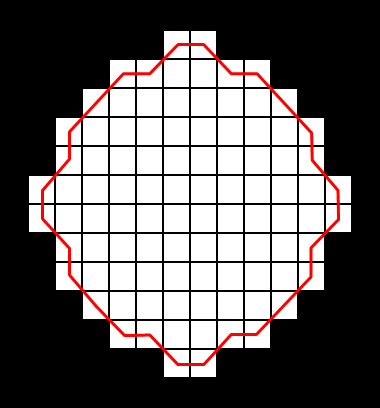
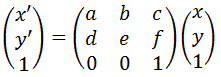
コメント
[…] 合、画素の画素の間の座標となってしまいますが、上図の例ではこの座標を四捨五入して輝度値を参照しているためで、bilinearやbicubicなどの補間を使うと少しは滑らかな画像となります。 […]