重心の計算方法

重心とは、重さの中心で、重心の位置で、力がつり合います。

重心の計算方法は、言葉で表すと

$$重心=\frac{（重さ\times位置）の合計}{重さの合計}$$

となります。

具体的な計算例を示すと、

のデータに関して、重心を計算すると、

$$重心=\frac{2\times0+5\times1+13\times2+15\times3+5\times4}{2+5+13+15+5}
=2.4$$

となります。

さらに二次元的な座標においても、各座標軸に関して、それぞれ計算を行います。

こちらも具体的に、以下のようなデータの場合、

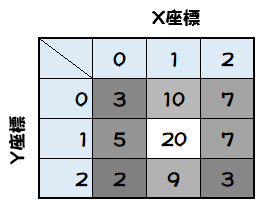
$$重心のx座標=\frac{3\times0+10\times1+7\times2+5\times0+20\times1+7\times2+2\times0+9\times1+3\times2}{3+10+7+5+20+7+2+9+3}$$

$$= 1.1$$

$$重心のy座標=\frac{3\times0+5\times1+2\times2+10\times0+20\times1+9\times2+7\times0+7\times1+3\times2}{3+5+2+10+20+9+7+7+3}$$

$$= 0.9$$

となります。（分母の重さの合計は、計算の順番が分かりやすいように、順番を入れ替えています。）

画像処理において重心を計算する場合は、重さの値に画像の輝度値を用いますが、二値化した画像に対して重心の計算を行い、重さを考慮しない場合もありますが、この場合は、重心の座標は、しきい値以上となる画素の座標の平均と一致します。