【OpenCV-Python】momentsによる重心の計算

画像処理において、重心は、欠陥部分の中心位置の算出や、レーザー光のように山なりの輝度分布を持つ画像の輝度値のピーク位置を求めるのに使っています。

重心の計算方法はこちらのページでも紹介しているように、計算そのものは、以下の計算式で求める事ができます。

$$重心=\frac{（重さ\times位置）の合計}{重さの合計}$$

ここで、画像処理における重さとは、画像の各画素の輝度値を差すので、

$$重心=\frac{（輝度値\times位置）の合計}{輝度値の合計}$$

となります。

OpenCVでは moments()関数を使って、重心を求めるのですが、OpenCVのページによると、モーメントは

$$m_{ji}=\sum_{x,y}(array(x,y)\cdot x^{j}y^{i})$$

で求められ、重心は

$$\overline{x}=\frac{m_{10}}{m_{00}},\overline{y}=\frac{m_{01}}{m_{00}}$$

となります。

と、書かれていいるのですが、式が何だか難しくて、よくわかりません。。

そこで、m00, m10, m01 を詳しく見ていきます。

m00は、

$$m_{00}=\sum_{x,y}(array(x,y)\cdot x^{0}y^{0})$$

$$=\sum_{x,y}(array(x,y)\cdot 1 \cdot 1)$$

$$=\sum_{x,y}(array(x,y))$$

となり、m00はarray(x,y)の合計ということがわかります。

array(x, y)は、位置が(x, y)の画素の輝度値を表しているので、m00 が画像の輝度値の合計となります。

m10は、

$$m_{10}=\sum_{x,y}(array(x,y)\cdot x^{1}y^{0})$$

$$=\sum_{x,y}(array(x,y) \cdot x \cdot 1)$$

$$=\sum_{x,y}(array(x,y) \cdot x )$$

となり、m10は画像の輝度値とx座標を掛け合わせた合計という事がわかります。

同様にm01は、

$$m_{01}=\sum_{x,y}(array(x,y)\cdot x^{0}y^{1})$$

$$=\sum_{x,y}(array(x,y) \cdot 1 \cdot y)$$

$$=\sum_{x,y}(array(x,y) \cdot y )$$

となり、m01は画像の輝度値とy座標を掛け合わせた合計という事がわかります。

ここで、重心は

$$重心のx座標=\frac{（輝度値\times x座標）の合計}{輝度値の合計}$$

$$重心のy座標=\frac{（輝度値\times y座標）の合計}{輝度値の合計}$$

となることから、重心の座標が

$$\overline{x}=\frac{m_{10}}{m_{00}},\overline{y}=\frac{m_{01}}{m_{00}}$$

で、求まる事が分かります。

実際のOpenCVで重心を求めるプログラムを示します。

画像全体の重心を求めるプログラム
画像の輪郭から重心を求める方法
輪郭から求める重心の座標について
参照ページ

画像全体の重心を求めるプログラム

import cv2

# グレースケールで画像を読み込む
img = cv2.imread("image.bmp", cv2.IMREAD_GRAYSCALE);

# 画像表示用に入力画像をカラーデータに変換する
img_disp = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)

# モーメントの計算
m = cv2.moments(img, False)
# 重心の計算
x,y= m['m10']/m['m00'] , m['m01']/m['m00']
print(f"Weight Center = ({x}, {y})")

# 座標を四捨五入
x, y = round(x), round(y)

# 重心位置に x印を書く
cv2.line(img_disp, (x-5,y-5), (x+5,y+5), (0, 0, 255), 2)
cv2.line(img_disp, (x+5,y-5), (x-5,y+5), (0, 0, 255), 2)

# 結果の表示
cv2.imshow("Image", img_disp)
cv2.waitKey()

実行結果

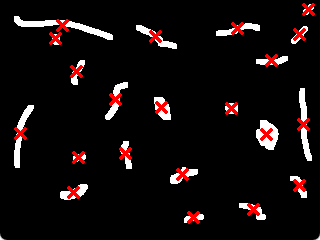
画像の輪郭から重心を求める方法

findContours()関数により、連続する領域の輪郭座標を求め、輪郭座標から、それぞれの重心を求めるには、以下のようにします。

import cv2

# グレースケールで画像を読み込む
img = cv2.imread("image.bmp", cv2.IMREAD_GRAYSCALE);

# 画像表示用に入力画像をカラーデータに変換する
img_disp = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)

# 二値化
ret,img = cv2.threshold(img,127,255,cv2.THRESH_BINARY)

# 輪郭情報の取得
contours, hierarchy = cv2.findContours(img, cv2.RETR_TREE, cv2.CHAIN_APPROX_NONE) 

# 輪郭ごとの処理
for i, contour in enumerate(contours):
    # 重心の計算
    m = cv2.moments(contour)
    x,y= m['m10']/m['m00'] , m['m01']/m['m00']
    print(f"Weight Center = ({x}, {y})")
    # 座標を四捨五入
    x, y = round(x), round(y)
    # 重心位置に x印を書く
    cv2.line(img_disp, (x-5,y-5), (x+5,y+5), (0, 0, 255), 2)
    cv2.line(img_disp, (x+5,y-5), (x-5,y+5), (0, 0, 255), 2)

# 結果の表示
cv2.imshow("Image", img_disp)
cv2.waitKey()

実行結果