3点,4点からなる二直線のなす角度を求めるというのは、以下の図のように、各点を通る二直線のなす角度を求める方法を紹介したいと思います。
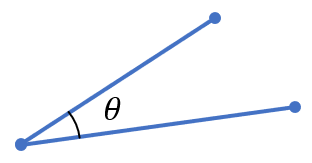
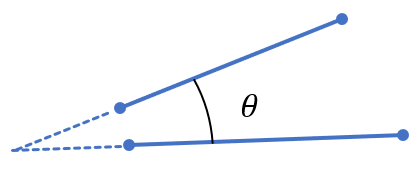
4点からなる二直線の角度は、2点が重なり合うように、直線を構成している2点を平行移動すれば、3点の場合と同じ様になるので、ここでは、3点からなる二直線のなす角度を求める方法で説明します。
普通のやり方
まず、最初に思いつくのが、2直線のそれぞれの線の傾きをアークタンジェントを使って求め、2つの角度の差を求める方法だと思います。
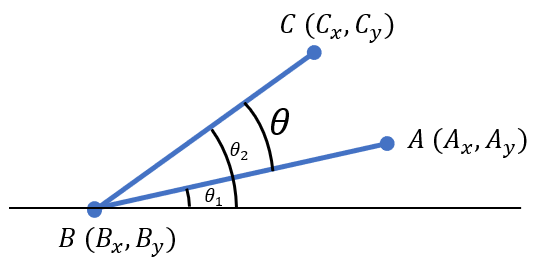
$$\theta_{1}=tan^{-1}(\frac{A_{y}-B_{y}}{A_{x}-B_{x}})$$
$$\theta_{2}=tan^{-1}(\frac{C_{y}-B_{y}}{C_{x}-B_{x}})$$
$$\theta = \theta_{2}-\theta_{1}$$
ただし、直線が垂直の場合、アークタンジェントの計算時の分母が0になり、0除算になってしまうため、プログラム上はアークタンジェントの関数は atan() を使うのではなく、 atan2()を使った方がいいです。
atan2()関数を使うと、戻り値が-180°~+180°となりますが、この180°の位置をまたぐ角度の算出には注意が必要です。
他にも、2直線のなす角度を求める方法として、内積、外積を使った方法があるので、これを紹介します。
内積を使った方法
2つの直線を下図のように2つのベクトルとして捉え、内積で角度を求めます。
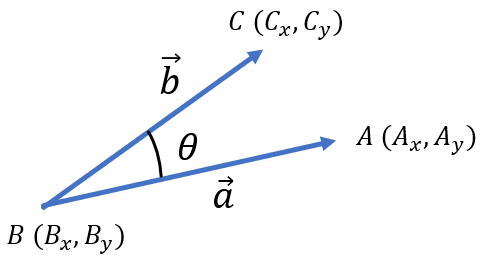
ベクトルa と ベクトルb を
$$\overrightarrow{a}=(a_{x}, a_{y}) = (A_{x}-B_{x}, A_{y}-B_{y})$$
$$\overrightarrow{b}=(b_{x}, b_{y}) = (C_{x}-B_{x}, C_{y}-B_{y})$$
とします。
ベクトルa と ベクトルb の内積は
$$\overrightarrow{a}\cdot \overrightarrow{b}=a_{x}b_{x} + a_{y}b_{y} = |\overrightarrow{a}||\overrightarrow{b}|cos\theta$$
であるから、式を変形して、
$$cos\theta=\frac{a_{x}b_{x} + a_{y}b_{y}}{|\overrightarrow{a}||\overrightarrow{b}|}$$
$$cos\theta=\frac{a_{x}b_{x} + a_{y}b_{y}}{\sqrt{{a_{x}}^{2}+{a_{y}}^{2}}\sqrt{{b_{x}}^{2}+{b_{y}}^{2}}}$$
$$\theta=cos^{-1}\left(\frac{a_{x}b_{x} + a_{y}b_{y}}{\sqrt{{a_{x}}^{2}+{a_{y}}^{2}}\sqrt{{b_{x}}^{2}+{b_{y}}^{2}}}\right)$$
として、角度θを求める事ができます。
ただし、アークコサインで求める事の出来る角度は0°~180°なので、マイナスの角度を求める事ができず、ベクトルbがベクトルaの右側か?左側か?の判断はできません。
右側か?左側か?の情報が必要な場合は、外積を用います。
外積を使った方法
外積については、少しおさらいです。
内積の結果はノルム(大きさ)となりますが、外積の結果はベクトルです。
外積の計算は
$$\overrightarrow{a}=(a_{x},a_{y},a_{z})$$
$$\overrightarrow{b}=(b_{x},b_{y},b_{z})$$
とすると、外積の結果は
$$\overrightarrow{a}\times \overrightarrow{b}=(a_{y}b_{z}-b_{y}a_{z},a_{z}b_{x}-b_{z}a_{x},a_{x}b_{y}-b_{x}a_{y})$$
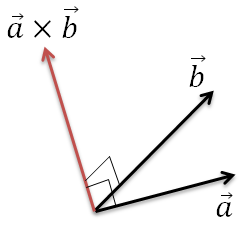
さらに、外積を行う2つのベクトルからなる平行四辺形の面積が、外積の大きさと一致します。
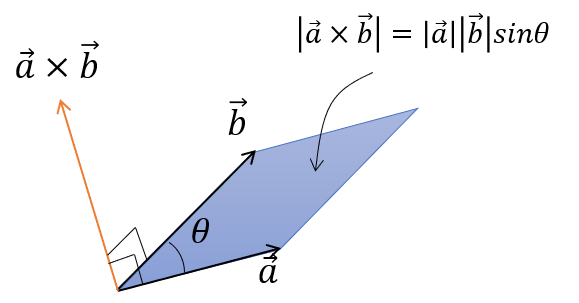
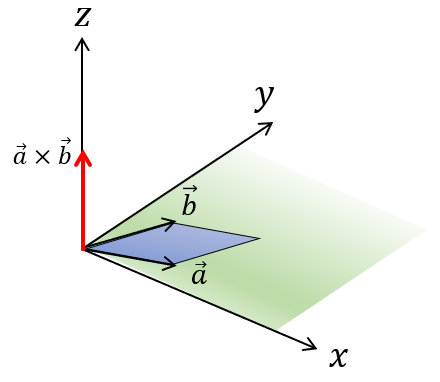
ここで、外積の計算は三次元ベクトルで行うのですが、外積を行う2つのベクトルのz成分を0にして、外積を計算すると、外積の結果の大きさは、外積の結果のz成分と一致します。
$$\overrightarrow{a}=(a_{x},a_{y},0)$$
$$\overrightarrow{b}=(b_{x},b_{y},0)$$
$$|\overrightarrow{a}\times \overrightarrow{b}|=a_{x}b_{y}-b_{x}a_{y}=|\overrightarrow{a}||\overrightarrow{b}|sin\theta$$
となります。
ここから式を変形して
$$sin\theta=\frac{a_{x}b_{y}-b_{x}a_{y}}{|\overrightarrow{a}||\overrightarrow{b}|}$$
$$sin\theta=\frac{a_{x}b_{y}-b_{x}a_{y}}{\sqrt{{a_{x}}^{2}+{a_{y}}^{2}}\sqrt{{b_{x}}^{2}+{b_{y}}^{2}}}$$
$$\theta=sin^{-1}\left(\frac{a_{x}b_{y}-b_{x}a_{y}}{\sqrt{{a_{x}}^{2}+{a_{y}}^{2}}\sqrt{{b_{x}}^{2}+{b_{y}}^{2}}}\right)$$
として、角度θを求める事ができます。
アークサインで求まる角度は-90°~90°となるので、ベクトルa と ベクトルb の位置関係を判断することができます。
θの値がプラスの場合、ベクトルb は ベクトルa に対して、反時計周りの位置にあります。
θの値がマイナスの場合、ベクトルb は ベクトルa に対して、時計周りの位置にあります。
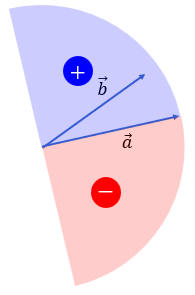
ただし、この計算だと±90°の範囲しか計算できませんが、その範囲以上の角度を求めたい場合は、ベクトルa と ベクトルb の内積の値も使います。
ベクトルa と ベクトルb の内積の値が正であれば、θは±90°の範囲内
ベクトルa と ベクトルb の内積の値が負であれば、θは±90°の範囲外
となるので、360°の範囲で、ベクトルa と ベクトルb の位置関係を求める事ができるようになります。
まとめ
●アークタンジェントで角度を求めるときは、atan()関数でなくatan2()関数を使う。
●内積や外積を使って角度を求めることもできる。
●内積だと、2つの直線の位置関係がわかりませんが、外積だと位置関係が分かる。
参考
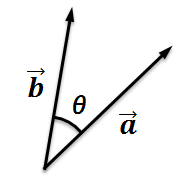



コメント