標準偏差とは?
標準偏差(Standard Deviation【略】SD)はデータの散らばりぐらいを示す値で σであらわされます。
測定誤差やノイズなどの評価値として用いられます。
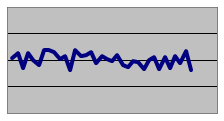
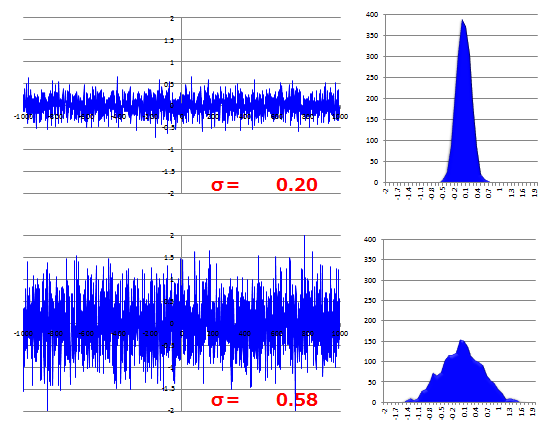
| 標準偏差(大) | 標準偏差(小) |
 |
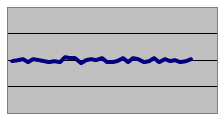 |
| データ | |
 |
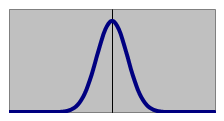 |
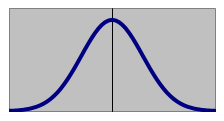
| ヒストグラム | |
標準偏差の計算
標準偏差は各データを![]() 、データの平均値を
、データの平均値を![]() とすると
とすると
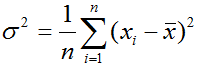
を分散といいます。分散の平方根
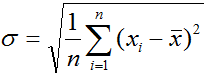
が標準偏差となります。
この式で数学的には問題は無いのですが、式を見ても分かるように全データから平均値を求めてから各データとの差を求めるため、プログラム的には全データを2回参照することになるため、あまりよろしくありません。
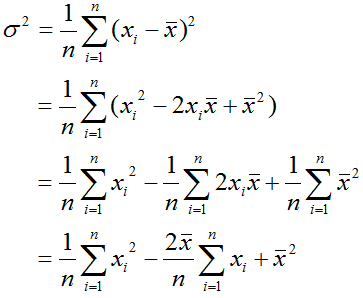
ここで平均値![]() は
は
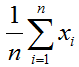
で求まることから、分散の式は
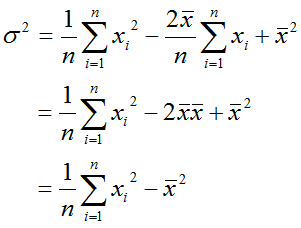
となり、この式を用いて分散、標準偏差のプログラムを作ると、全データを1回の参照で済むので、より効率的になります。
ポイント!!
分散 = 2乗の平均 - 平均の2乗
標準偏差 = 分散の平方根
正規分布
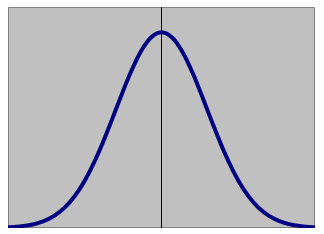
下図のように、平均値付近にデータの出現頻度が集中し、頻度に偏りが無く、平均値に対して左右対称で、平均値から遠くなればなるほど頻度が少なくなる状態を
「正規分布にしたがう」といいます。
この頻度を関数であらわすと
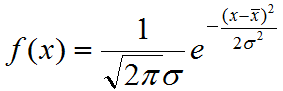
となります。
正規分布はガウス分布とも呼ばれ、画像処理のフィルタ処理にも使われます。
正規分布にしたがう場合のデータは下図のような割合で分布します。
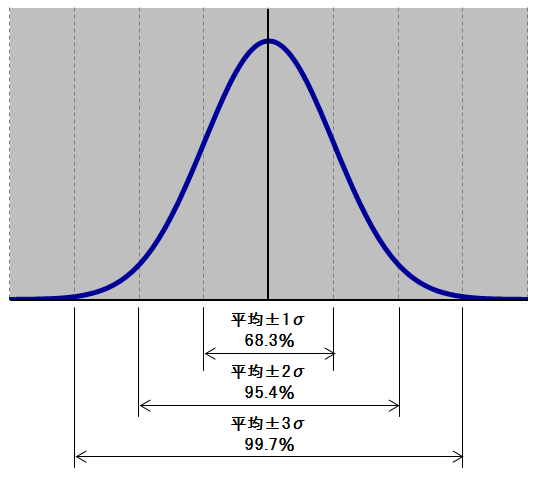
この特性から、測定器の測定精度やカメラで撮影した画像のノイズレベルなどにおいて1σや3σなどであらわされる場合があります。
実際に標準偏差を用いる場合の注意点についても以下のページにまとめましたので、合わせてご覧頂けると幸いです。
まとめ
標準偏差の計算は、計算の式を暗記しようとするのではなく、計算の方法を言葉で覚える事をおススメします。
そうすると、必然的に標準偏差が何を計算しているのか?理解できるようになると思います。
分散はデータと平均の差の二乗の平均
分散の平方根が標準偏差
分散の計算のプログラムは
分散 = 2乗の平均 - 平均の2乗
で求める。


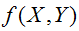
コメント
[…] 標準偏差の説明としては、 […]
[…] でも、この式もどこかで見たことがあるな~と思っていたら、正規分布の式で見たことがあります。 […]