前回紹介したGauss-Jordan法で解く逆行列の計算では例えば、

のように対角要素に0(ゼロ)が来ると、0で割れないため、対角要素を1にする事ができません。
そこで、対角要素に0(ゼロ)が来ないように行を入れ替えてGauss-Jordan法を行います。
さらに、ある値を割る場合、分母の値は絶対値が大きい方が割り算の誤差が小さくなります。
(この割る要素の事をピボット(pivot)と言います。)
この事を考慮し、Gauss-Jordan法で逆行列を求める例を示します。
行列の右側に単位行列を追加します。
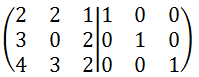
1行1列目の要素の絶対値が最大となるように1行目と3行目を入れ替えます。
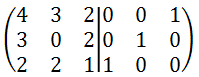
1行1列目の要素が1となるように1行目を4で割ります。
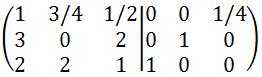
1列目の要素が(1 0 0)となるように
[2行目] = [2行目]ー[1行目]×3
[3行目] = [3行目]ー[1行目]×2
を計算します。
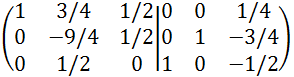
ここで2行2列目の要素の絶対値はすでに最大なので、2行2列目の要素が1となるように
2行目を-9/4で割ります。
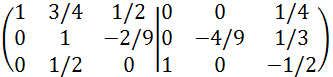
2列目の要素が(0 1 0)となるように
[1行目] = [1行目]-[2行目]×3/4
[3行目] = [3行目]-[2行目]×1/2
を計算します。
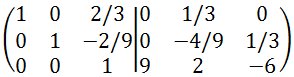
ここで、3行3列目の要素はすでに1なので、3列目の要素が(0 0 1)となるように
[1行目] = [1行目]-[3行目]×2/3
[2行目] = [3行目]+[3行目]×2/9
を計算します。
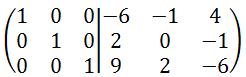
これで、左側が単位行列となり、右側に出来た行列が求める逆行列となります。
このようにピボット選択を考慮する事で、対角要素が0であっても逆行列を解くことが可能となる場合があります。

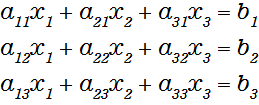
コメント
[…] 5/12 ピボット選択を行ったGauss-Jordan法 […]
[…] 5/12 ピボット選択を行ったGauss-Jordan法 […]