ロバストとは?
ロバスト(Robust)という言葉を辞書で調べると、「頑健なさま、がっしりした様子」という意味が載っています。
画像処理的には、ノイズや影、明るさの変動などの影響を受けにくく、安定した処理結果が得られる、ぐらいの意味として捉えれば良いでしょう。
ロバスト推定法
通常の最小二乗法では下図のように、数点の大きな誤差が含まれるだけでも、近似した直線が大きくズレてしまう場合があります。
この誤差の影響をできるだけ受けないようにしたのが、ロバスト推定法です。
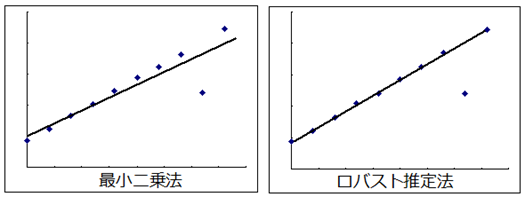
処理アルゴリズム
まずは最初に、通常の最小二乗法を行います。
(今回は簡単にするため一次式で近似する例で紹介します。)
直線の式(y=ax+b)で近似する場合は以下のように行列を用いて解くことができます。
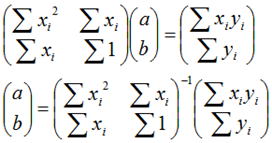
この近似した直線から遠く離れたデータを除去するだけでも、大きな誤差のデータの影響を受けなくなりそうですが、ここでは、誤差の大きさに応じて重みを付けるTukeyのBiweight推定法という手法を紹介します。
近似データ(Xi、Yi)と近似直線との誤差 d=Yi – (aXi + b) を用いて、誤差が大きければ大きいほど、
最小二乗に与える影響力(重み)が小さくなるように、以下のような式を用いて重み計算します。
d < -Wの場合
![]()
-W <= d <= Wの場合
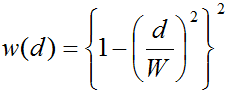
W < dの場合
![]()
ただし、大文字のWは誤差の許容範囲を示します。
この重みの関数w(d)をグラフで示すと、このようになります。
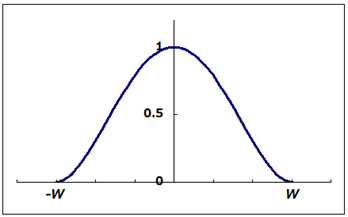
上図を見ても分かるように誤差の絶対値がWを超えると重みが0となり、次に行う重み付き最小二乗法では近似に影響を与えなくなり、逆に誤差が0に近づく程、重みが増し、近似への影響が大きくなります。
この重み wi を各近似データ(Xi、Yi)に関して計算し、wiを付加した最小二乗法を再度行います。
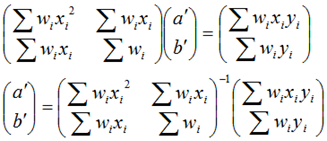
こうして求めた近似式(y = a’X + b’)は最初に求めた近似式よりも、測定データに近づきます。
この処理を誤差の許容範囲(W)を小さくしながら、誤差が少なくなるまで繰り返すことで、より測定データに近づいた近似式を得ることができます。
今回の例では一次式について示していますが、他のn次式などについても、同様に行列の各要素に重みを付加することで、ロバスト推定を行うことができます。
参考文献



コメント
[…] 7/14 ロバスト推定法(Tukey’s biweight) […]