単位ベクトルとその応用

単位ベクトルとは？長さが１のベクトルとなります。

例えば、ベクトルa の要素を

としたときの単位ベクトルu は

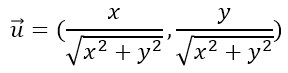
となります。

これを図示すると、

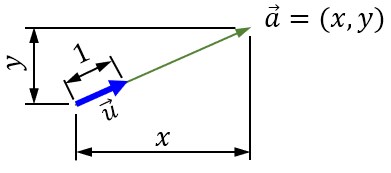
のようになります。

これを学生の時に教わったときには簡単！とだけ思っていましたが、大人になると、

で、単位ベクトルの何がいいの？？

となります。

しかし、実は、単位ベクトルには教わった記憶の無い（少なくとも覚えていない）大事な特徴がありました。
それは

単位ベクトルと任意ベクトルの内積を計算すると、
単位ベクトル方向の成分（大きさ）が取得できる！

ということです。

例えば、ベクトルa の単位ベクトルu の方向の成分は、ベクトルa と単位ベクトルu の内積の絶対値で求まります。

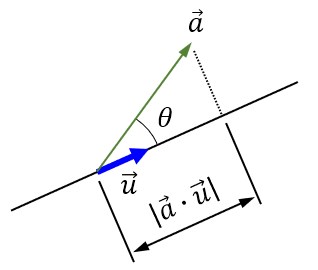
なぜ、そうなるのか？は比較的簡単で、ベクトルa の単位ベクトルu の方向の大きさを L として、ベクトルa の単位ベクトルu の成す角をθとして、図示すると

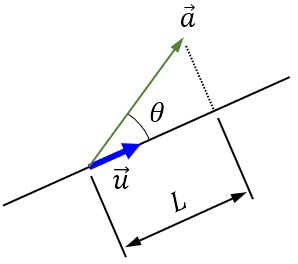
となります。

Lは図から

となるのは、図を見れば分かると思います。

ここで、ベクトルa と単位ベクトルu の内積は

となりますが、単位ベクトルの大きさは 1 なので、

となり、先ほどの L と一致する事が分かります。

ちなみに、θの角度が 90° ～270°の範囲の場合、cosの値がマイナスとなるため、ベクトルu の方向の大きさを求める場合は、内積の絶対値を求めています。

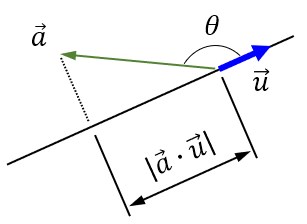
また、あえて絶対値を取らないで、内積が正の場合は、ベクトルa は単位ベクトルu の向きの方向にあり、内積が負の場合はベクトルa は単位ベクトルu の逆向きになっていることを確認する事もあります。

これを応用すると、内積は二次元のベクトルだけではなく、３次元、４次元・・・とｎ次元ベクトルに拡張できるので、応用範囲は広くあります。

例えば三次元ベクトルの場合ですが、三次元平面と点の距離を求める方法について説明したいと思います。

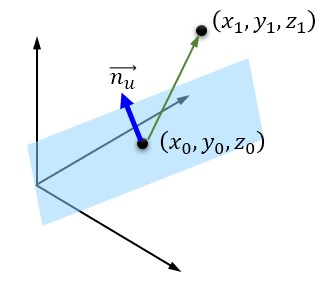
平面の方程式は

のように表されますが、この法線ベクトルｎ は

となります。

この法線ベクトルの単位ベクトルは、各要素を大きさで割って

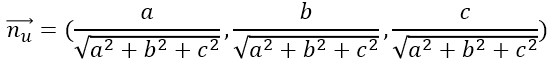
となります。

あとは、平面上の点（x₀, y₀, z₀）と任意の点（x₁, y₁, z₁）からなるベクトル

との内積を計算すると、

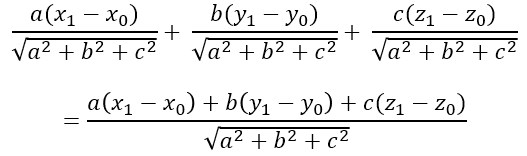
となって、この値の絶対値を取ると平面と点との距離となります。

逆に絶対値を取らないと、値が正の場合、点は法線ベクトルの方向にあり、値が負の場合は点が法線ベクトルとは逆の方向にある事が分かります。値が０の場合は、点は平面上にある事になります。

 

まとめ

・単位ベクトルと任意ベクトルとの内積を計算すると、単位ベクトル方向の大きさを求めることができる。

というのが、大事な特徴です。

私が大人になってから単位ベクトルを使った事があるのは、平面と点との距離のように、単位ベクトルの方向の大きさを求めるような使い方しかないかも？
広い意味で言うと、フーリエ変換も単位ベクトルが係わっていたりもしますが。。