フーリエ変換に関しては
と説明してきて、ようやく本題の離散フーリエ変換(DFT:Discrete Fourier Transform)となりました。
いきなり離散フーリエ変換って何?と思われる事もあるかと思いますが、画像や音声、AD信号などのデータに対するフーリエ変換は離散フーリエ変換となります。
フーリエ変換と言えば、FFTの方が有名ですよね。FFTは、Fast Fourier Transformの略で、日本語では高速フーリエ変換となります。このFFTは、データの個数を2のn乗個に制限することで、高速に処理を行う処理アルゴリズムであって、基本的には離散フーリエ変換を行っています。
そのため、いきなりFFTを理解するのではなく、まずは離散フーリエ変換を理解すると、FFTの理解も深まります。
そこで以下については、離散フーリエ変換にいての説明です。
フーリエ変換に関しては、数々の説明が本やHPでされていますが、なかなか理解するには至らず、ここでは私なりの理解で説明したいと思います。
説明の途中でベクトルという言葉が出てきますが、厳密なベクトルではなく、複素数のイメージで説明しているように複素数を指している場合があるので、ご了承下さい。
e(ネイピア数)を使った説明
※e(ネイピア数)を使わない説明は後半に記載しました。
ここで、いきなり離散フーリエ変換の公式ですが、主に以下の3つの公式を目にします。

どの公式もΣ以降は同じで離散フーリエ変換はeの指数部分がマイナス、逆離散フーリエ変換のeの指数部分がプラスとなっています。
異なるのはΣの頭に付く係数のみです。
3つも公式を並べると、どれを使えばいいの?みたいに思われるかもしれませんが、どれの公式も正解で使う公式によってパワースペクトルの大きさが異なってきますが、各周波数によって得られるパワースペクトルの相対的に大きさには変わりがありません。
しかし、最初の式だけはパワースペクトル(振幅スペクトル)の値に意味を持つので、最初の式を用いて説明します。
※一般には2番目の式が用いられる場合が多いです。(エクセルも2番目の式となります)
| 【Memo】 離散フーリエ変換を行った結果[F(t)]は複素数となります。 この複素数の絶対値(大きさ)を振幅スペクトルと言います。 振幅スペクトルを2乗したものがパワースペクトルとなります。 |
まず、公式のf(x)がフーリエ変換を行うデータの配列で、データ個数がN個となります。
tが周波数に近い値で全データ中に含まれる波(1周期分の波)の数を表し、データの個数と同じ0~N-1分だけ波が存在します。
フーリエ変換を行った結果F(t)はある特定の周波数tの時の結果で、やはり0~N-1分だけの結果が存在し、この結果は複素数となります。
それでは離散フーリエ変換の詳細を見てみたいと思います。
まず、フーリエ変換の公式の複素数(eiθ)の部分に着目します。
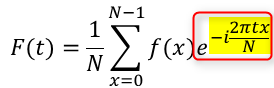
これを見ると複素数のイメージの部分でも説明しましたが、θの部分が
\(\theta=-\frac{2\pi tx}{N}\)
ですが、x はデータのインデックス番号(0, 1, 2…, N-1)で、Nはデータの個数となっています。
これを少々変形し、
\(\theta=-2\pi t\frac{x}{N}\)
とすると、x/Nの部分は、N個のデータ全体(0, 1, 2,…,N-1)が、0~1になるように調整されているので、tの値により、θの範囲が変わります。
t = 0 のとき、θ = 0
t = 1 のとき、0<= θ < -2\(\pi\)
t = 2 のとき、0<= θ < -4\(\pi\)
t = 3 のとき、0<= θ < -6\(\pi\)
:
となります。
つまり、複素空間におけるベクトルがtの値により時計周り(回転角度が負の方向)にt回転するイメージです。
こんな感じ↓
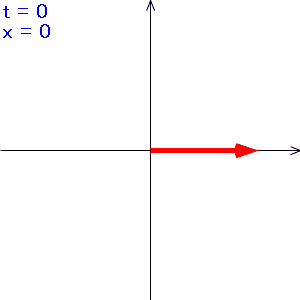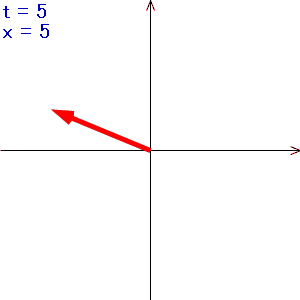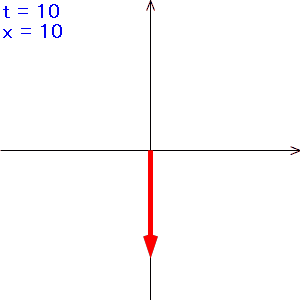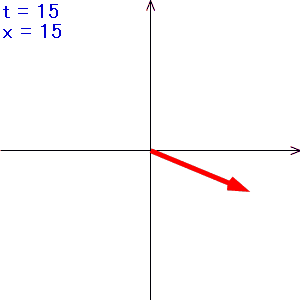
tの値が大きくなると矢印の回転も速くなっていくのですが、途中から回転が逆になり、遅くなるように見えます。
この現象はちょうど、走っている車のタイヤをビデオカメラで撮影すると、タイヤが途中で止まって、さらに車の速度が速くなると、タイヤが逆転するように見えるのと似ています。
次にf(x)の部分に着目すると複素数(eiθ)の頭の部分にf(x)が付いているので、各xに対応した複素数の大きさ(ベクトル)がf(x)倍される事になります。
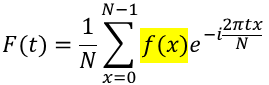
最後にΣでN個の値を合計して、Nで割っているので、複素数を平均している事が分かります。
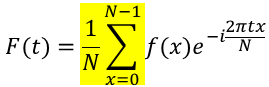
ここで、データの個数が16個だけの簡単な例を示します。
f(0)~f(15)のデータを以下のようにします。
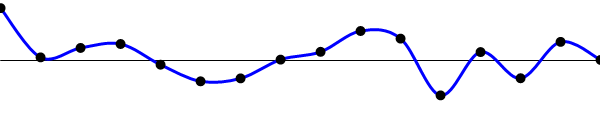
このデータを周波数t(0~15)ごとに離散フーリエ変換を行います。
(この結果がF(0)~F(15))
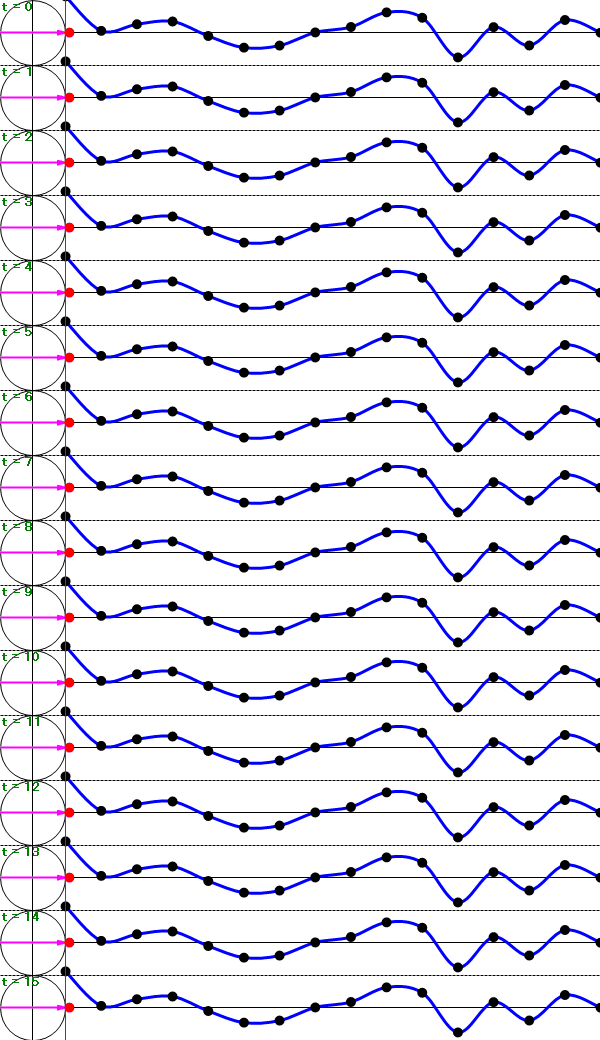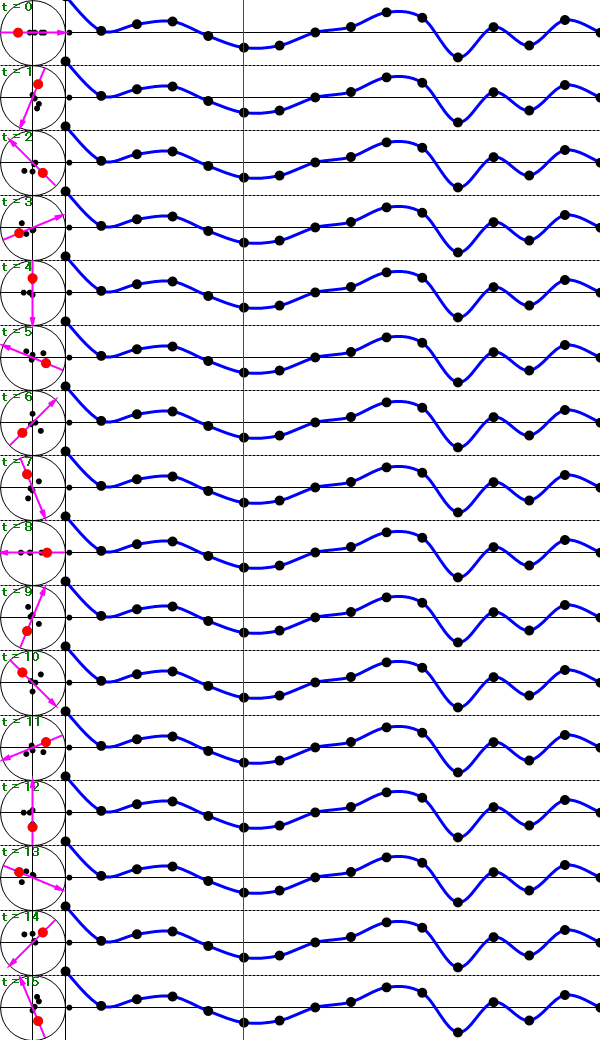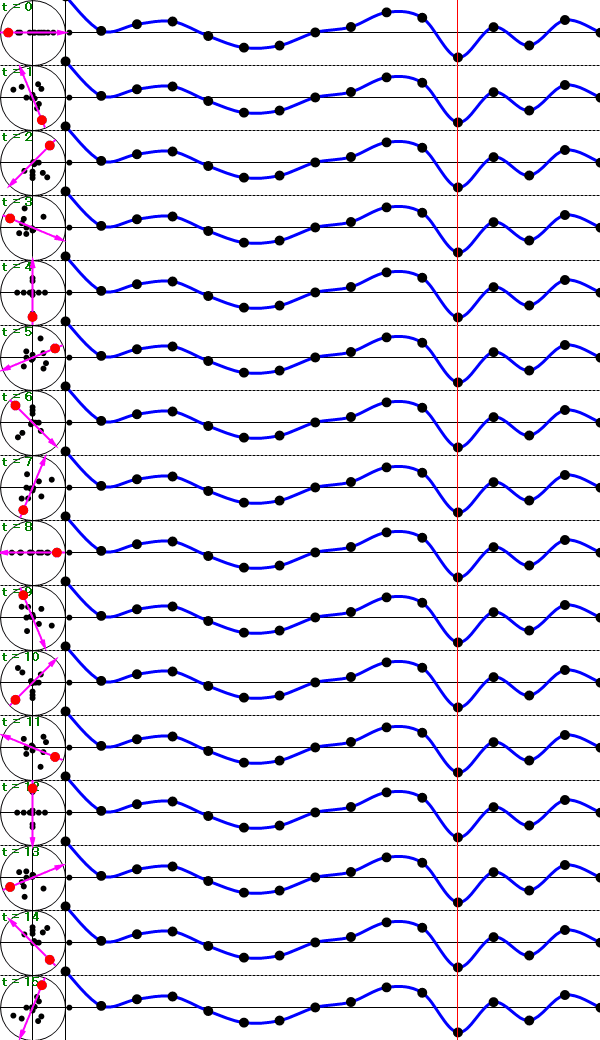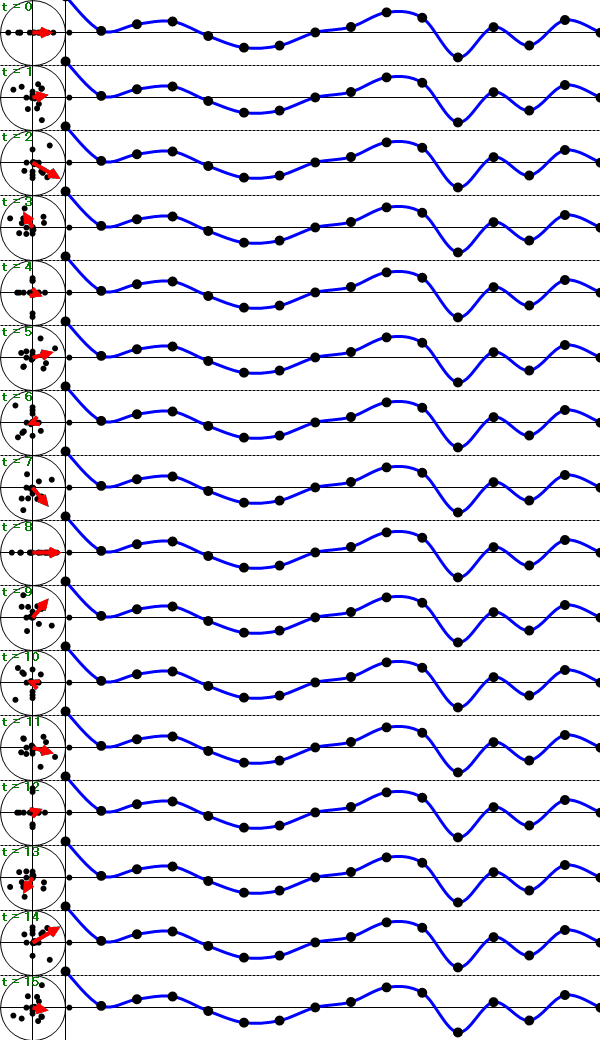
上図のように、複素平面に変換されたデータ(左側の黒い点)の平均へ向かうベクトル(赤い矢印)こそが、離散フーリエ変換した結果となります。
つまり、離散フーリエ変換の結果は各周波数ごとの複素数となります。
このベクトル(赤い矢印)の大きさが各周波数における波形の大きさ(振幅スペクトル)でベクトルの向きが各周波数の位相となります。
ただし、一般に、この振幅スペクトルは各周波数の波形の振幅ではない事にご注意下さい。
ここで着目して頂きたいのが、t=7 と t=9、t=6 と t=10、t=5 と t=11・・・がベクトル(赤い矢印)の大きさ同じで位相(ベクトルの向き)が±逆となる組み合わせが存在しています。
さらにもう少し詳しく見ていきます。
フーリエ変換とは?のページで紹介してますが、任意の波形を以下のように定めます。
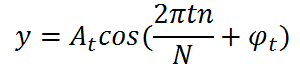
ただし、
N:データ個数
t = 0、1、2、・・・・N-1
n = 0、1、2、・・・・N-1
At:tの時の振幅
φt:tの時の位相
t:データ全体に含まれる1周期分の波の個数。この値で周波数を調整します。
この時、波形の位相φが変化すると、フーリエ変換を行うと、どのように変化するのか?
周波数t=2の時、位相を変えながらフーリエ変換を行う例を以下に示します。
上図の左側が複素平面で右側が実数平面です。
当然ながら、途中に出てくるベクトル(赤い矢印)の角度(位相)が変化します。
次に振幅を変えるとどうなるか?やってみると
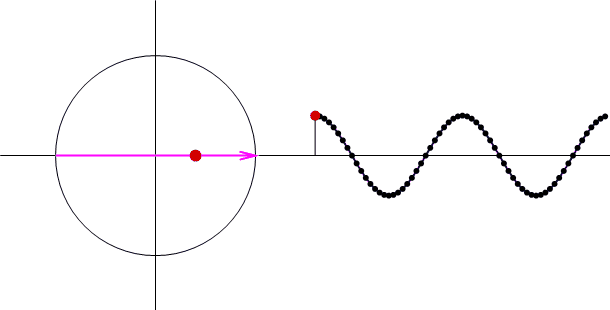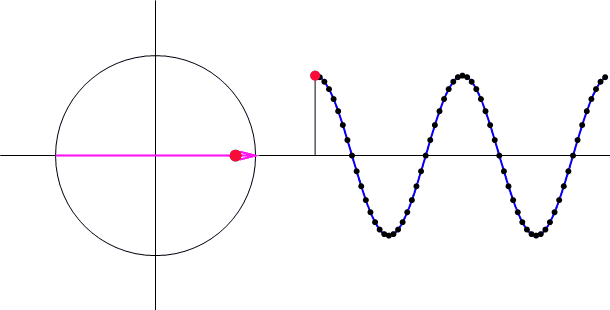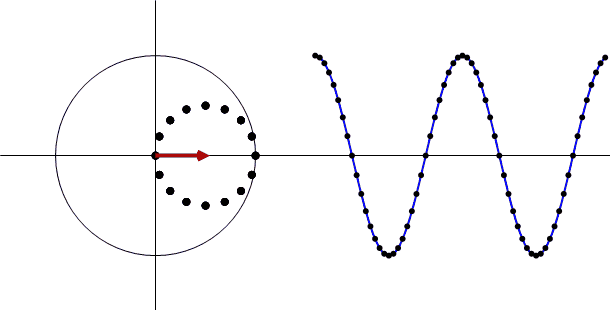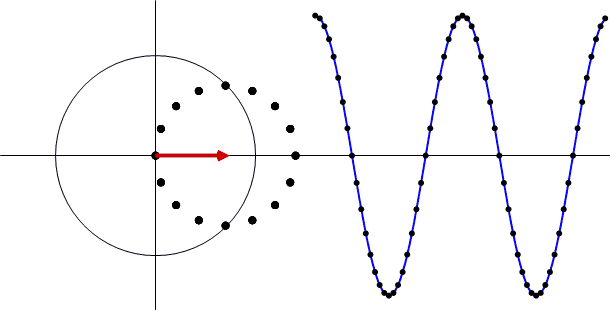
途中に出てくるベクトル(赤い矢印)の大きさ(振幅スペクトル)が変化します。
この振幅スペクトルの大きさが、本記事の上部で紹介している離散フーリエ変換の公式の一番最初に出てくる公式を用いると、振幅スペクトルの大きさは信号の振幅の半分の大きさになるのが、好きなとこ。
ここまでは、普通な感じでしょうか。
次からが、フーリエ変換を使う大事なところ!?
離散フーリエ変換を行う特定の周波数(ここではt = 2の時)に着目し、それ以外の周波数の信号をフーリエ変換するとどうなるのか?見てみると...
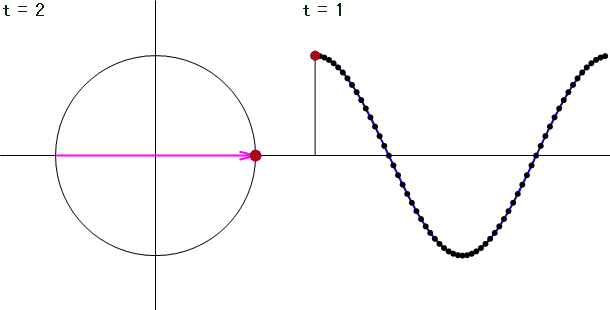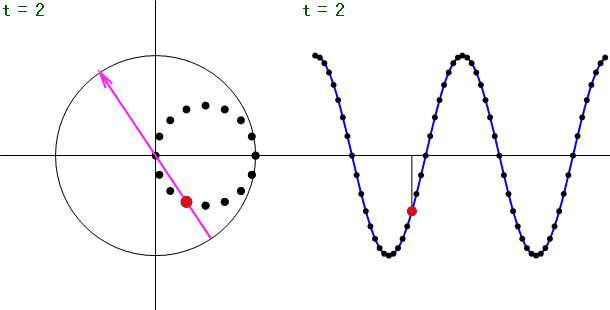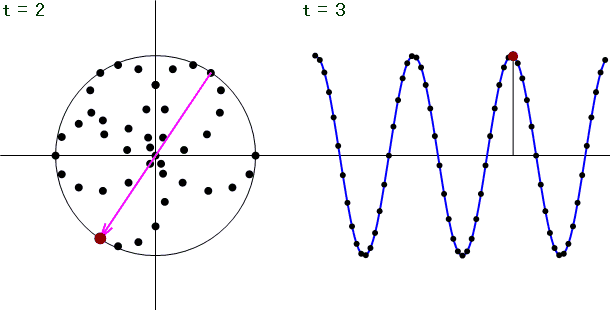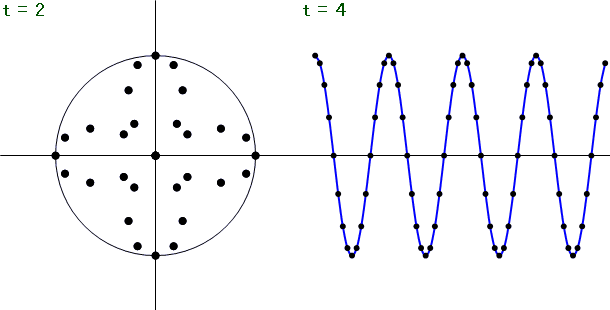
上図のように、信号の周波数とフーリエ変換を行う周波数とが一致した時のみ振幅スペクトルが出現し、それ以外は振幅スペクトルの大きさが0となります。
上図を見ても分かるように、周波数が一致しないと、複素平面上で中心から放射状にデータを打ち消しあう作用が働き、特定の周波数のみの成分を抽出する事が可能となります。
この辺が、フーリエ変換に複素数を使うのが好きなところ。
今度は、各データにバイアス成分というか、直流成分というか、ただのオフセットを加えて変化させてみます。
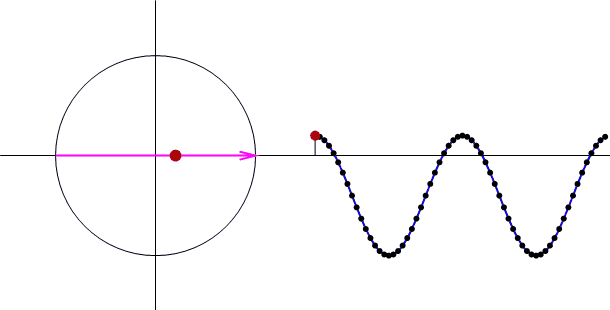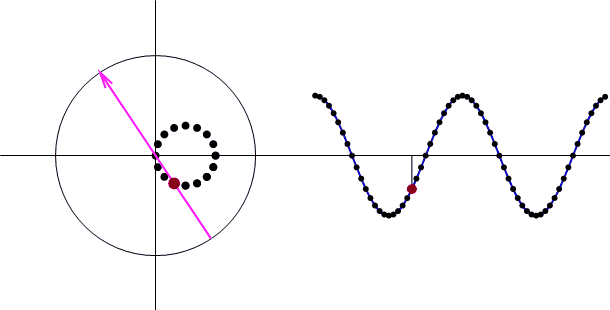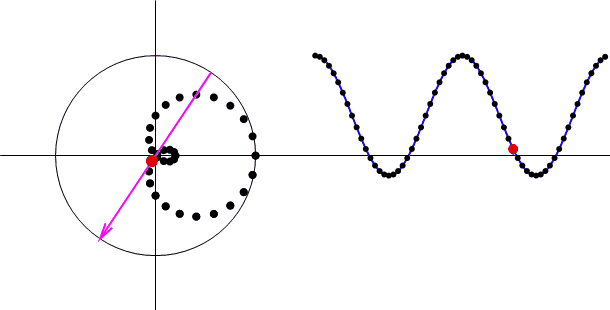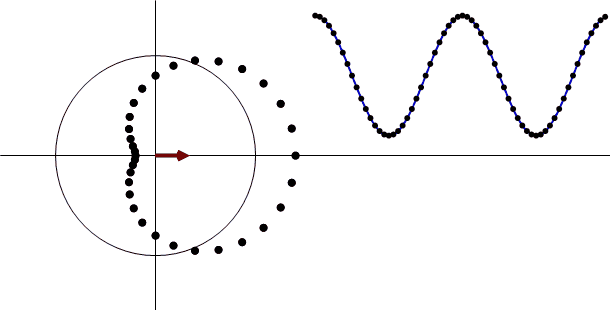
途中に出てくるベクトル(赤い矢印)の大きさ(振幅スペクトル)が変化しません!
つまり、信号の周波数が分かっていれば、バイアス成分の影響を受ける事なく、信号の位相を抽出する事ができます。
この性質は、フーリエ変換の位相を使った処理では大事なところです。
さらに、周波数t=2の時の例を示してきましたが、この信号に周波数t=2以外の信号を加えたら、周波数t=2の時のフーリエ変換がどうなるか?見ていきます。
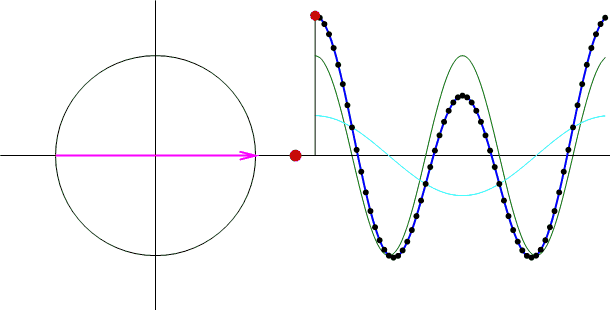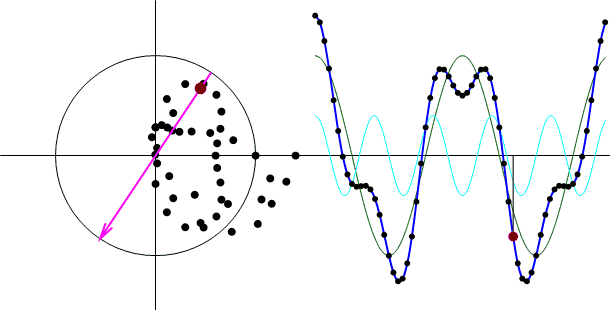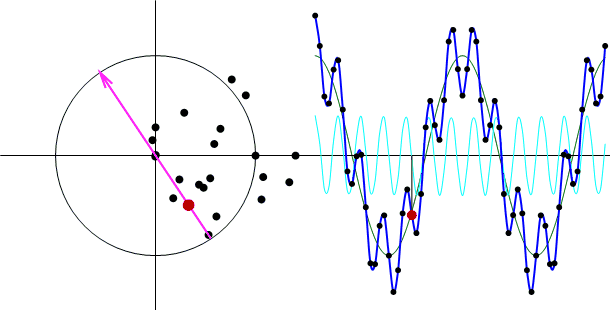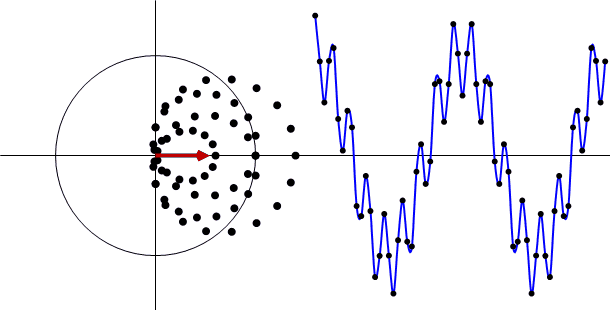
上図右側の緑色の線が周波数t=2の信号、水色の線が周波数t=2以外の信号、
青色の線が足し合わせた信号です。
これを見てもやはり、途中に出てくるベクトル(赤い矢印)の大きさ(振幅スペクトル)が変化しません!
もはや複素平面の黒い点はバラバラに見えるのですが、他の周波数の影響を受けずに周波数t=2の信号成分のみを抽出してくれています。
この性質が、よくフーリエ変換を行って、各周波数の振幅スペクトルを解析する事で、周波数の特性を使った処理に使われる要因です。
ただし、ここで挙げている例は、少し意図的な部分もあって、合成している波形は全て整数倍で示される周波数の波形を足し合わせた例を示しています。
しかし、実際の信号では、必ずしも整数倍の周波数となる訳もなく、整数倍でない周波数が加わると、複素平面の円の放射方向にデータを打消し合わないなので、振幅スペクトルにも影響が出るのでご注意下さい。
と、フーリエ変換については、少し前までは、各周波数成分との正規直交との射影をとる事で、各周波数成分を抽出する!ぐらいの認識でいたのですが、これだといまいちビジュアル的にイメージできません。
ここに書いてあるイメージだと、なんだかよく分からなかった複素数もビジュアル的にイメージできて、ようやくフーリエ変換を理解できた気になってます。
ちなみに、このフーリエ変換のイメージ、自称 ぐるぐるフーリエ変換
e(ネイピア数)を使わない説明
eを使うと、数式的にはシンプルに書けますが、実際のプログラムではeを使えない場合も多いので、sinとcosを使った説明をしたいと思います。
離散フーリエ変換は、例えば、周波数が1の場合は、全データをちょうど1回転するようにデータをぐるぐる、複素平面へ変換し、変換したデータの平均(平均すると、実数成分と虚数成分の2つ出てきます)が周波数1の時の離散フーリエ変換の結果となります。
周波数が2の時は、全データをちょうど2回転するようにデータを変換し、平均します。
下図は周波数が2の場合を示していますが、この変換を周波数0~N-1(Nはデータ個数)まで行います。

ぐるぐる回す、つまりデータを回転させているのですが、回転といえば、画像処理をしているとアフィン変換に出てくる回転行列がありますよね。
$$\left( \begin{matrix} { { x }^{ ‘ } } \\ { y }^{ ‘ } \end{matrix} \right) =\begin{pmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{pmatrix}\left( \begin{matrix} x \\ y \end{matrix} \right) $$
離散フーリエ変換における\(x\)と\(y\)は何に相当するか?というと\(x\)が実部、\(y\)が虚部となります。
そのため、\(n\)番目の実部データを\({ Re }_{ n }\)、\(n\)番目の虚部データを\({ Im }_{ n }\)、周波数\(t\)の時の\(n\)番目の角度を\({ \theta t }_{ n }\)とすると、実部と虚部のデータの回転を行列で表すと
$$\left( \begin{matrix} { { Re }_{ t,n }^{ ‘ } } \\ { Im }_{ t,n }^{ ‘ } \end{matrix} \right) =\begin{pmatrix} cos{ \theta t }_{ n } & -sin{ \theta t }_{ n } \\ sin{ \theta t }_{ n } & cos{ \theta t }_{ n } \end{pmatrix}\left( \begin{matrix} { Re }_{ n } \\ { Im }_{ n } \end{matrix} \right) $$
となります。
周波数\(t\)の時の\(n\)番目の角度\({ \theta t }_{ n }\)は、データの個数Nの全体で1周期分、2周期分…となるように調整し、
$${ \theta t }_{ n }=-2\pi t\frac { n }{ N } $$
となります。離散フーリエ変換の場合(逆離散フーリエ変換ではなく)、回転方向がマイナス方向(時計回り)になるため、角度の頭にマイナスが付きます。
この \({ { Re }_{ t,n }^{ ‘ } }\) と \({ { Im }_{ t,n }^{ ‘ } }\) の\(n\)について、0~N-1の値を平均すると、周波数\(t\)の時の離散フーリエ変換後の値が求まります。
周波数\(t\)の時の離散フーリエ変換後の
実部は
$$\frac { 1 }{ N } \sum _{ n=0 }^{ N-1 }{ { Re }_{ t,n }^{ ‘ } } =\frac { 1 }{ N } \sum _{ n=0 }^{ N-1 }{ \left\{ cos\left( -2\pi t\frac { n }{ N } \right) \times { Re }_{ n }-sin\left( -2\pi t\frac { n }{ N } \right) \times { Im }_{ n } \right\} } $$
虚部は
$$\frac { 1 }{ N } \sum _{ n=0 }^{ N-1 }{ { Im }_{ t,n }^{ ‘ } } =\frac { 1 }{ N } \sum _{ n=0 }^{ N-1 }{ \left\{ sin\left( -2\pi t\frac { n }{ N } \right) \times { Re }_{ n }+cos\left( -2\pi t\frac { n }{ N } \right) \times { Im }_{ n } \right\} } $$
となります。
あとは周波数\(t\)に関して t = 0 ~ N-1 の時の実部と虚部の値を求めると、各周波数ごとの実部と虚部の成分が求まります。
残すは周波数ごとの実部と虚部の値から、大きさと位相に変換する場合が多いのですが、これは三平方の定理的に考えればいいだけなので簡単です。
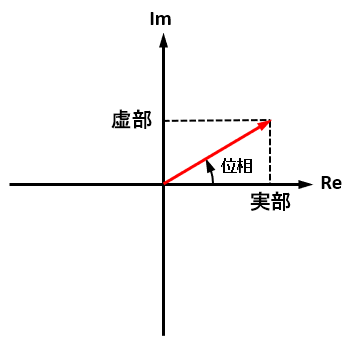
$$大きさ=\sqrt { { 実部 }^{ 2 }+{ 虚部 }^{ 2 } } $$
$$位相={ tan }^{ -1 }\frac { 虚部 }{ 実部 } $$
となります。
これで以上ですが、実際の離散フーリエ変換では、二次元フーリエ変換でもない限り?変換する元のデータの虚部(Im)は0(ゼロ)の場合が多いので、プログラム的には
実部を
$$\frac { 1 }{ N } \sum _{ n=0 }^{ N-1 }{ { Re }_{ t,n }^{ ‘ } } =\frac { 1 }{ N } \sum _{ n=0 }^{ N-1 }{ \left\{ cos\left( -2\pi t\frac { n }{ N } \right) \times { Re }_{ n } \right\} } $$
虚部を
$$\frac { 1 }{ N } \sum _{ n=0 }^{ N-1 }{ { Im }_{ t,n }^{ ‘ } } =\frac { 1 }{ N } \sum _{ n=0 }^{ N-1 }{ \left\{ sin\left( -2\pi t\frac { n }{ N } \right) \times { Re }_{ n } \right\} }$$
として計算する場合もあります。
まとめ
以上のように、離散フーリエ変換はデータを周波数に合わせてグルグル巻きにして平均を計算します。
1周期の成分は、全データを1回転させて平均する。
2周期の成分は、全データを2回転させて平均する。
3周期の成分は、全データを3回転させて平均する。
・・・
のようにします。
この時、平均した位置と原点までの距離がその周波数の大きさ、X軸と原点ー平均の位置のなす角度が位相になります。フーリエ変換では、何かと大きさばかりに注目されがちですが、位相も有用です。
周波数という言葉を使うと単位はHz(1/秒)?と思ってしまうかもしれませんが、記事中では厳密な使い方をしていません。単位が必要な場合は、全データを何秒でサンプリングしたのか?が重要になってきます。
例えば、全データを2秒でサンプリングした場合は、
1周期と言っていた周波数は、2秒で1回転するので、0.5Hzとなります。
同様に2周期の場合は2秒で2回転するので1Hz
3周期の場合は2秒で3回転するので1.5Hz
となります。
実際のところ、個人的にはFFTや離散フーリエ変換を画像処理に使う機会は、ほとんどありません。
0~N-1周期分の全てのデータが必要ではなく、ある特定の周波数成分はどの程度あるのか?みたいな使い方は良くします。
そのためFFTよりも離散フーリエ変換の方を部分的に使う事が多いので、ぜひ、離散フーリエ変換を理解して応用できるようになって欲しい!という思いで、この記事を書きました。
←フーリエ変換へ戻る


コメント
最近はハムトランシーバにウォーターフォールと云うスペクトルとオシロが同時に表示される便利なスコープが搭載されて居ます。XY軸がスペアナ、Z軸にオシロ表示される物です。Z軸が斜め上から視た表現に成って居ます。立体的に視れる物です。
[…] 離散フーリエ変換(DFT:Discrete Fourier Transform) | イメージングソリューション […]
長年理解をあきらめていた、フーリエ変換のイメージを短時間でつかめました。
非常に感謝しています。
masaさん、コメント頂きありがとうございます。
私自身も、ここに書いてあるイメージに至るまでは、かなり遠回りして来ましたが、ここのイメージでようやくフーリエ変換が腑に落ちた気になっています。
[…] ーリエ変換を行うのが離散フーリエ変換となります。 […]
[…] 8/29 離散フーリエ変換 […]