C#にはアフィン変換に用いる行列用の
Matrixクラス(名前空間:System.Drawing.Drawing2D)
というクラスがあり、これを駆使すると、以下のようなプログラムを比較的簡単に作成することができます。

プログラムの実行ファイルはこちらより→ AffineImage101.zip
ソースコードはGitHubで公開しています。
プログラムの機能としては
- 画像ファイルのDrag&Dropで画像をピクチャボックス全体に表示
- マウスのドラッグで表示画像の移動
- マウスホイールの回転でマウスポインタを中心に画像の拡大縮小
- マウスホイールの回転 + Shiftキー でマウスポインタを中心に画像の回転
- マウスのダブルクリックで画像をピクチャボックス全体に表示
- ステータスバーにマウスポインタのピクチャボックス座標と、画像上の座標を表示
となります。
ここで用いていたMatrixクラスの主なメソッドは
| Translate | 平行移動 |
| Scale | 拡大縮小 |
| RotateAt | 指定した点を中心に回転 |
| Reset | リセット、単位行列の代入 |
| Invert | 逆行列を求める |
| TransformPoints | 点の配列をアフィン変換する |
となります。
ただ、これだけだと少し物足りないので、以下のメソッドを拡張メソッドとして追加しています。
| ScaleAt | 指定した点を中心に拡大縮小 |
| ZoomFit | 画像をピクチャボックスの大きさに合わせる |
以下、ソースコードの解説です。
アフィン変換行列に基づいて画像の表示
DrawImageメソッド(名前空間:System.Drawing)には、描画する画像の領域と、描画先の座標を画像の左上、右上、左下の順でPointFの配列で指定することで、画像を任意場所や大きさで表示することが可能となります。
この描画先の座標をアフィン変換行列で求めて画像を表示しています。
public static void DrawImage(this Graphics g, Bitmap bmp, System.Drawing.Drawing2D.Matrix mat)
{
if ((g == null) || (bmp == null))return;
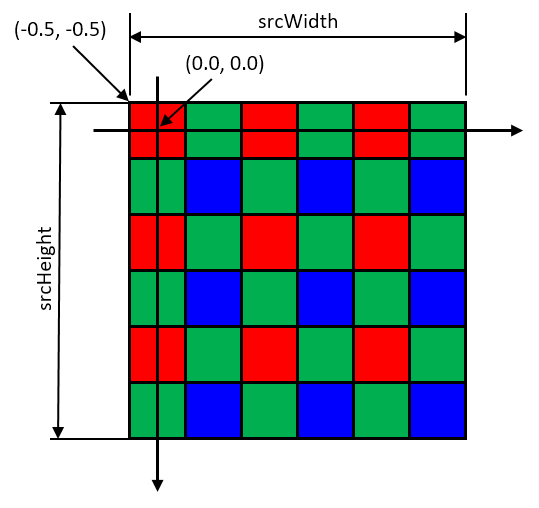
// 画像の画素の外側の領域
var srcRect = new RectangleF(
-0.5f,
-0.5f,
bmp.Width,
bmp.Height
);
// 画像の左上、右上、左下の座標
var points = new PointF[] {
new PointF(srcRect.Left, srcRect.Top), // 左上
new PointF(srcRect.Right, srcRect.Top), // 右上
new PointF(srcRect.Left, srcRect.Bottom)// 左下
};
// アフィン変換で描画先の座標に変換する
mat.TransformPoints(points);
// 描画
g.DrawImage(
bmp,
points,
srcRect,
GraphicsUnit.Pixel
);
}
ただし、画像の左上の座標は(-0.5, -0.5)となるのでご注意下さい。
(参考)
指定した点を中心に拡大縮小
アフィン変換で行う拡大縮小の変換行列は座標の原点を中心に拡大縮小するため、単に拡大縮小のアフィン変換行列を掛けただけでは、意図しない拡大縮小となります。
そこで、アフィン変換を組み合わせて、
中心座標を原点へ移動→拡大縮小→原点から元の位置へ移動
の変換を行うと、指定して点中心の拡大縮小となります。
public static void ScaleAt(this System.Drawing.Drawing2D.Matrix mat, float scale, PointF center)
{
// 原点へ移動
mat.Translate(-center.X, -center.Y, System.Drawing.Drawing2D.MatrixOrder.Append);
// 拡大縮小
mat.Scale(scale, scale, System.Drawing.Drawing2D.MatrixOrder.Append);
// 元へ戻す
mat.Translate(center.X, center.Y, System.Drawing.Drawing2D.MatrixOrder.Append);
}
(参考)
画像をピクチャボックスに合わせて表示する
ここでのアフィン変換の考え方は、まず、画像の左上の座標をピクチャボックスの原点に合わせるため、(+0.5, +0.5)だけ平行移動(Translate)します。
↓ (+0.5, +0.5)だけ平行移動
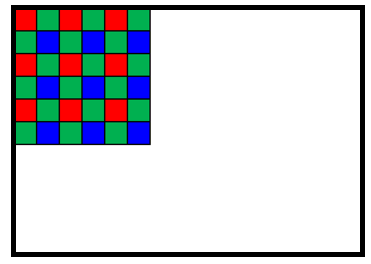
次に、画像の縦横比とピクチャボックスの縦横比を比較して、画像が縦長の場合、画像の縦の長さとピクチャボックスの縦の長さが揃うように画像を拡大縮小(Scale)します。
画像が横長の場合は、横の長さが合うように画像を拡大縮小(Scale)します。
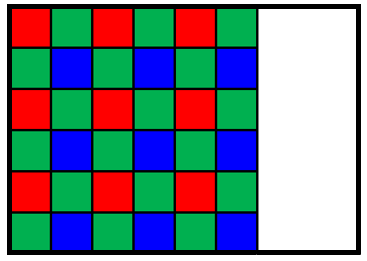
最後に、画像がピクチャボックスの中心に来るように平行移動(Translate)します。
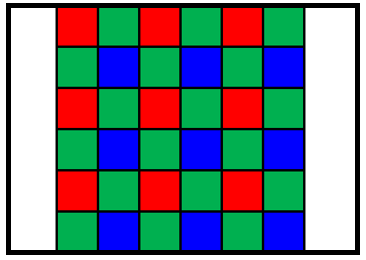
public static void ZoomFit(this System.Drawing.Drawing2D.Matrix mat, PictureBox pic, Bitmap bmp)
{
if (bmp == null) return;
// アフィン変換行列の初期化(単位行列へ)
mat.Reset();
// 0.5画素分移動
mat.Translate(0.5f, 0.5f, System.Drawing.Drawing2D.MatrixOrder.Append);
int srcWidth = bmp.Width;
int srcHeight = bmp.Height;
int dstWidth = pic.Width;
int dstHeight = pic.Height;
float scale;
// 縦に合わせるか?横に合わせるか?
if (srcHeight * dstWidth > dstHeight * srcWidth)
{
// ピクチャボックスの縦方法に画像表示を合わせる場合
scale = dstHeight / (float)srcHeight;
mat.Scale(scale, scale, System.Drawing.Drawing2D.MatrixOrder.Append);
// 中央へ平行移動
mat.Translate((dstWidth - srcWidth * scale) / 2f, 0f, System.Drawing.Drawing2D.MatrixOrder.Append);
}
else
{
// ピクチャボックスの横方法に画像表示を合わせる場合
scale = dstWidth / (float)srcWidth;
mat.Scale(scale, scale, System.Drawing.Drawing2D.MatrixOrder.Append);
// 中央へ平行移動
mat.Translate(0f, (dstHeight - srcHeight * scale) / 2f, System.Drawing.Drawing2D.MatrixOrder.Append);
}
}
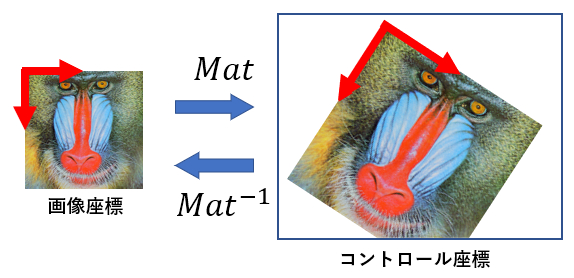
ピクチャボックスの座標から、元の画像の座標を求める
これまで説明してきたアフィン変換の行列は、画像の座標をピクチャボックスの座標へ変換するためのアフィン変換行列を求めています。
それでは、その逆のピクチャボックスの座標を元の画像の座標へ変換するには、アフィン変換行列の逆行列を求めて座標変換することで、元の画像を求める事ができます。
この処理をサンプルプログラムでは、MouseMoveイベントで行っています。
その一部抜粋です。
private void picImage_MouseMove(object sender, MouseEventArgs e)
{
////////////////////////////
// マウスポインタの座標と画像の座標を表示する
// マウスポインタの座標
lblMousePointer.Text = $"Mouse {e.Location}";
// アフィン変換行列(画像座標→ピクチャボックス座標)の逆行列(ピクチャボックス座標→画像座標)を求める
// Invertで元の行列が上書きされるため、Cloneを取ってから逆行列
var invert = _matAffine.Clone();
invert.Invert();
var pf = new PointF[] { e.Location };
// ピクチャボックス座標を画像座標に変換する
invert.TransformPoints(pf);
// 画像の座標
lblImagePointer.Text = $"Image {pf[0]}";
}
(参考)

以上、如何だったでしょうか?
「アフィン変換」と言うと、「えっ?行列の計算??」「なんか難しそう」と言われて何かと敬遠されがちなのですが、アフィン変換に少し慣れると、計算も比較的スッキリとするかと思います。
私からすると、ここでやっている計算を幾何学的に求めようとすると、そっちの方がはるかに大変。。
画像をピクチャボックスに合わせて表示するで紹介しているようにアフィン変換行列を一発で求めようとするのではなく、変換前の状態から変換後の状態へと変換するまでの手順を考え、その手順を行列で表して掛けていく部分がポイントとなります。
アフィン変換の行列の計算部分では、画像そのものを拡大縮小/平行移動している訳ではなく、たかだか3x3の行列の積を計算しているだけなので、計算量としても少なくて済みます。
←画像処理のためのC#テクニックへ戻る

コメント
Akiraさま
表示倍率の求め方、ご提示ありがとうございます。
ヘッダー表示部に組み込んで倍率が表示されるのを確認しました。
拡大・縮小範囲判定の方も差し替えすることにします。
2値フォーマットの件、申し訳ありません。勘違い、というか
今回の描画処理自体とは何ら関係がありませんでした。
実は、読み込んだ画像に文字列を上書き表示する処理を独自に追加しています。
その処理の中で例外が発生するので、回避のためにあらかじめPixcelFormatを
置き換える処理が必要になりました。
文字列追記処理を通さなければ例外発生しませんでしたので、指摘ミスです。
因みに、ご質問の画像ファイル由来ですが、jpg形式で、
Canonのスキャナで取り込み、スキャナ付属ソフトの
MP Navigator EXでファイル化したものです。
とりあえず、何とかなりそうで良かったです。
自作の画像表示ソフトに拡大鏡画面が欲しくて、こちらにたどり着きました。
ソースコードは少ないですし、描画速度は速いです。
拡張メソッドの書き方は知りませんでしたので勉強になりました。
良質なコードの公開、ありがとうございます。
私の用途で例外で落ちる箇所が2点見つかりましたのでレポートします。
・縮小し過ぎ
例外で落ちるので、拡大・縮小回数チェックを入れました。
元画像が極小だと、このやり方では回避できなそうですが、自分用なので
良しとしました。
・2値の画像フォーマットが利用できない
ライブラリ内で例外になるので、事前に内部でフォーマット変換して
差し替える処理を入れました。
-imageにbitmapをコピーする際、以下の関数を噛ませています。
public void copybmpPage(Bitmap magbmp)
{
if (_image != null) _image.Dispose();
if ((magbmp.PixelFormat & PixelFormat.Indexed) != 0)
{
// ライブラリ側が上の条件でエラーにするので、強制的にフォーマットを変更する
RectangleF cloneRect = new RectangleF(0, 0, magbmp.Width, magbmp.Height);
System.Drawing.Imaging.PixelFormat format = PixelFormat.Format8bppIndexed;
_image = magbmp.Clone(cloneRect, format);
}
else
{
_image = magbmp;
}
}
評価頂きありがとうございます。
スケールが小さい時には確かに逆行列を求める部分でエラーがでますね。
(仕事では、似たような事をやっているのですが、MinScaleなるプロパティで最小表示倍率を制限していたりもします。)
表示倍率ですが、
var scale = Math.Sqrt(_matAffine.Elements[0] * _matAffine.Elements[0] + _matAffine.Elements[1] * _matAffine.Elements[1]);
とすると、表示倍率が求まりますので、この値で、縮小の制限をかけて頂ければ良いかと思います。
画像の回転をしないのであれば、_matAffine.Elements[0]の値がそのまま表示倍率となります。
二値画像フォーマットが表示できない件については、Windowsのペイントで作成したFormat1bppIndexedフォーマットのビットマップファイル(*.bmp)を開いた時はエラーが出なかったのですが、二値画像のファイルフォーマットは何で、どのソフトを使って作成されましたでしょうか?
いつも困ったときに参考にさせて頂いています。
大きい画像(8192*500)をマウスホイールで拡大した場合に、表示が間に合わない症状が発生します。フォームの拡大縮小を行うとリフレッシュの影響なのか全表示が行われます。
画像サイズが大きいので処理が間に合わずにDraw関数を抜けてしまうのでしょうか?
問題ない場合もあるのでタイミング的な影響?と疑いたくなるのですが、色々試してみたのですが原因が判明しません。
コメントありがとうございます。
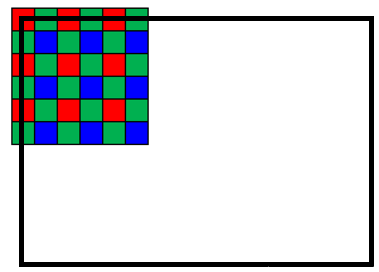
ここでのサンプルでは、内容を簡単にするため大きい画像の時の表示は、あまり考慮していないのですが、大きい画像を拡大して表示するときは、表示するピクチャボックスに対して、かなりはみ出した状態で表示しています。
そのため、表示ができなかったり、例外でプログラムが落ちる場合があるのですが、大きい画像の拡大表示を考慮する場合は、このページに書いてある DrawImageのメソッドを少し工夫する必要があります。
このメソッド内の points の部分がPictureBoxへの描画先の領域になりますが、この座標がピクチャボックスからはみ出すときに、表示する画像を部分的に切り出すようにして画像を表示します。
具体的にはアフィン変換行列で使っている mat の逆行列を使って、ピクチャボックスの角の座標が、元の画像のどの座標になるのか?を求めます。
この求めた座標から、描画する画像の部分的な領域(srcRect) を求めて、さらにsrcRect の領域が、ピクチャボックス上のどの座標(points)になるのか?を求めて画像を表示するようにします。
座標の細かい調整が必要になるかも?しれませんが、頑張ってみてください。
とても参考になりました。
一点、90度以上回転させると縮小ができなくなるようです。
グリグリ回って頭が混乱するのですが(笑)、頑張って
対策考えてみようと思います。
ご指摘ありがとうございます。
確かに縮小出来なくなりますね。
ちょっと確認してみます。
とりあえず修正しました。
原因は、画像の拡大/縮小をするとき、倍率で制限をするために表示倍率を取得するために、アフィン変換行列の1行1列目の要素のみを参照していたためでした。
回転を考慮すると、それだけでは不十分なため、もう少しちゃんと計算しないといけないのですが、複雑になってしまうため、とりあえず倍率制限の部分を削除しました。