例えば、下図のように2x2画素の画像を4x4の画像に拡大する場合、アフィン変換を使えばいいんでしょ!と、安易に考えていると、思わぬ落とし穴があったりもします。
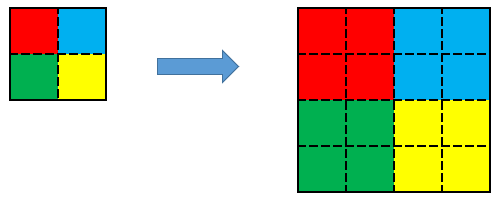
大事なポイントとして、
●画像の座標の原点は左上の画素の中心が原点(0.0、0.0)となる。(例外もあります)
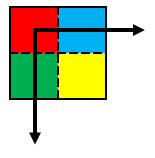
●アフィン変換の拡大縮小は原点を基準として拡大縮小される。
となります。
これを気にせず、ただ、アフィン変換で画像を2倍に拡大すると、左上の画素の中心を基点に画像が拡大されます。
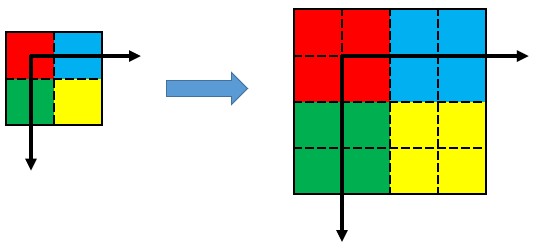
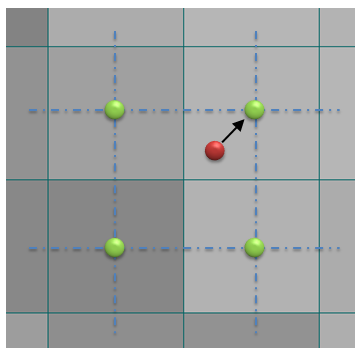
これで、一見良さそうにも感じるのですが、拡大後の画像において、画素の中心が原点であることから、4x4画素の領域は下図の四角で示した領域であり、画像全体が左上に0.5画素ズレた状態になっていまいます。
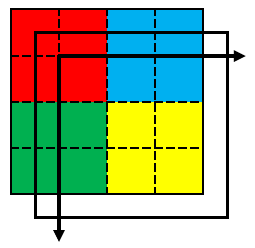
アフィン変換で画像を拡大する時の変換前と変換後の状態は、以下のようになるのが正解です。
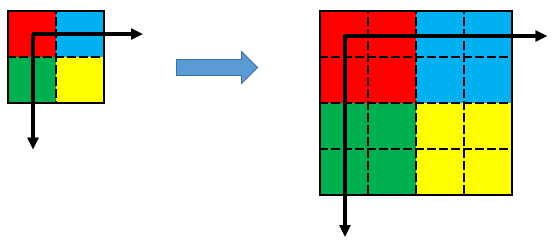
この変換をアフィン変換で実現するには以下のように行います。
変換前の状態

| ①画像全体を右下に(+0.5,+0.5)画素移動 | |
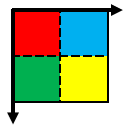 |
$$\begin{pmatrix} 1 & 0 & 0.5 \\ 0 & 1 & 0.5 \\ 0 & 0 & 1 \end{pmatrix}$$ |
|
②画像を2倍に拡大 |
|
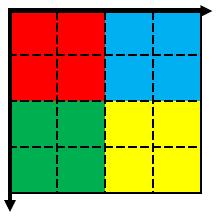 |
$$\begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix}$$ |
|
③画像全体を左上に(-0.5,-0.5)画素移動 |
|
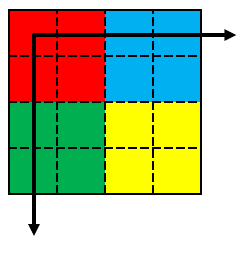 |
$$\begin{pmatrix} 1 & 0 & -0.5 \\ 0 & 1 & -0.5 \\ 0 & 0 & 1 \end{pmatrix}$$ |
となります。
この一連の変換をアフィン変換行列であらわすと
$$\begin{pmatrix} { x }^{ ‘ } \\ { y }^{ ‘ } \\ 1 \end{pmatrix}=\begin{pmatrix} 1 & 0 & -0.5 \\ 0 & 1 & -0.5 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 & 0.5 \\ 0 & 1 & 0.5 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\\ \\ $$
$$\begin{pmatrix} { x }^{ ‘ } \\ { y }^{ ‘ } \\ 1 \end{pmatrix}=\begin{pmatrix} 2 & 0 & 0.5 \\ 0 & 2 & 0.5 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}\\ \\ $$
となり、単に拡大のアフィン変換行列だけを掛ければOKでは無いことが分かります。
ちなみに、C#で2x2画素の画像をPictureBoxのSizeModeプロパティをZoomにして、ImageプロパティにBitmapを設定すると、このようになります。
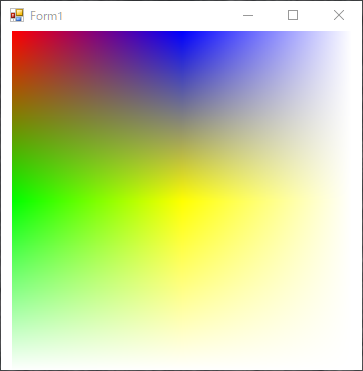
なんとなく、画像が左上にズレているようで、なんか怪しい!!
【関連記事】
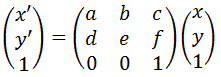

←画像処理のためのC#へ戻る



コメント
間違っていると思います。
拡大で、原点(0, 0) が (0.5, 0.5) になるはずがありません。
原点は不動点であるはずです。これでは、座標計算ができません。
そもそも、画素を「マス目」で考えていることが、間違いのもとだと思います。
画素は「点」で考えるべきだと思います。
横レス失礼します。
記事は『原点がずれる』とも『マス目の左上角を座標とする』とも『基本演算はこうあるべきである』とも言っていないのですが。
・「スケーリング200%ならにじまない」と言っている人がナイーブに想定しているのは『2×2の4画素が1画素として使われる』状況で、記事はこういうニーズを教科書どおりに扱ったらどうなるかを示したものです。
・この手順によれば、(0,0)-(1,1)の画像の重心(0.5,0.5)を(0,0)-(3,3)の領域の重心(1.5,1.5)に写すことになるので、その意味で自然な処理であると言えます。この言い方ならマス目が関係ないのは分かりますね?
dummy_indexさん。
補足頂きありがとうございました。