C#では複素数を扱う Complex構造体(名前空間:System.Numerics)が用意されています。
ただし、プロジェクトの初期状態では、使えないため、プロジェクトの参照を右クリックし、参照の追加で System.Numerics を追加してください。
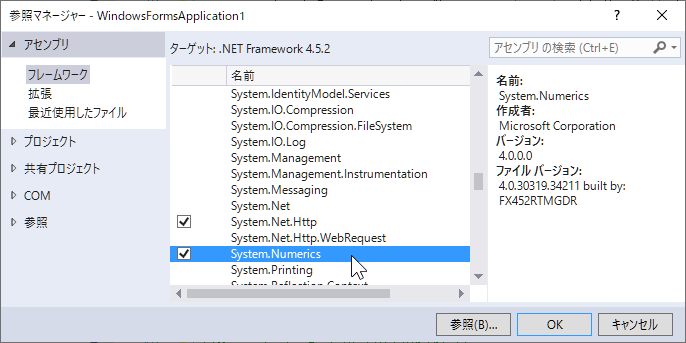
コード例
var complex1 = new System.Numerics.Complex(Math.Sqrt(3), 1.0);
Console.WriteLine($"complex1.Magnitude = {complex1.Magnitude}");
Console.WriteLine($"complex1.Phase = {complex1.Phase * 180.0 / Math.PI}");
var complex2 = new System.Numerics.Complex(1.0, Math.Sqrt(3));
Console.WriteLine($"complex2.Magnitude = {complex2.Magnitude}");
Console.WriteLine($"complex2.Phase = {complex2.Phase * 180.0 / Math.PI}");
var complex3 = complex1 * complex2;
Console.WriteLine($"complex3.Magnitude = {complex3.Magnitude}");
Console.WriteLine($"complex3.Phase = {complex3.Phase * 180.0 / Math.PI}");
var complex4 = complex1 + complex2;
Console.WriteLine($"complex4.Magnitude = {complex4.Magnitude}");
Console.WriteLine($"complex4.Phase = {complex4.Phase * 180.0 / Math.PI}");
// 結果
//complex1.Magnitude = 2
//complex1.Phase = 30
//complex2.Magnitude = 2
//complex2.Phase = 60
//complex3.Magnitude = 4
//complex3.Phase = 90
//complex4.Magnitude = 3.86370330515627
//complex4.Phase = 45
複素数の大きさは Magnitudeプロパティで、位相はPhaseプロパティで拾えるし、複素数の演算(加算、減算、乗算、除算)も可能です。
複数の演算は、複素数と複素数、複素数と実数の演算が可能です。
これが出来るという事はDFT(離散フーリエ変換)も簡単に出来ちゃいますね。
関連ページ
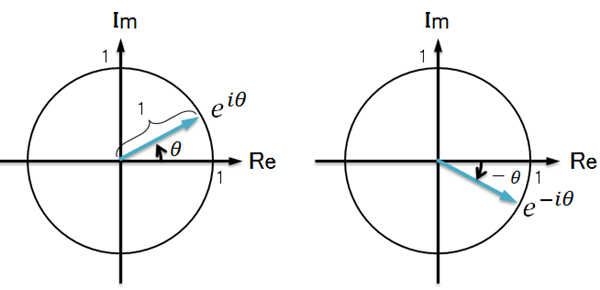
複素数のイメージ
離散フーリエ変換を勉強すると、突然eiθ = cosθ + i sinθみたいな式が突然出てきて、これが何だかよく分からないまま、とりあえず公式だけを覚えてみたり...しかも i は「実際には存在しない虚数」みたいに教わったので、存在しな...
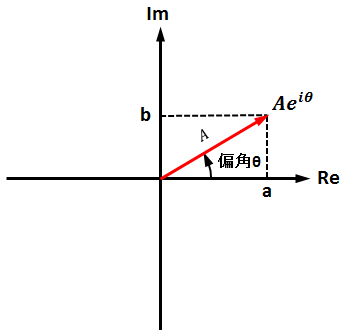
複素数の計算
複素数については実在しないものの様に教わったので、なかなか理解できないままでいたのですが、実際に使ってみると便利に感じることもあるので、数学的には厳密でないかもしれませんが、私なりの理解でまとめてみます。結論からすると、複素数は複素平面(横...

離散フーリエ変換(DFT)
フーリエ変換に関しては フーリエ変換とは? フーリエ変換の種類 複素数のイメージと説明してきて、ようやく本題の離散フーリエ変換(DFT:Discrete Fourier Transform)となりました。いきなり離散フーリエ変換って何?と思...
参考ページ

Complex 構造体 (System.Numerics)
複素数を表します。
← C# へ戻る


コメント