画像を回転する場合、任意点周りの回転移動でも紹介したように回転行列を使って、例えば、画像の中心周りに画像を回転させると、下図のように回転後の画像が虫食い状態になってしまいます。
 |
→ |  |
| 回転前の画像 | 回転後の画像 |
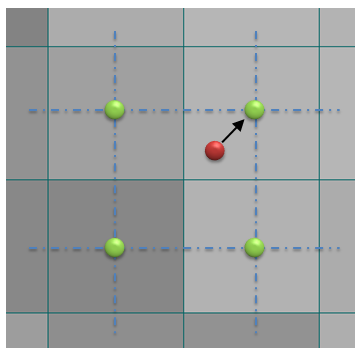
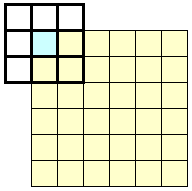
こうならないようにするためには、回転前の画像の座標を回転行列を使って回転後の座標を計算するのではなく、回転後の座標が回転前の画像のどの座標を参照しているのかを計算し、画像を変換します。
つまり、画素を置きに行くのではなく、拾いに行くようにします。
【回転前の画像を回転行列を使って変換】

【回転後の座標が回転前のどの座標を参照しているかを計算して変換】
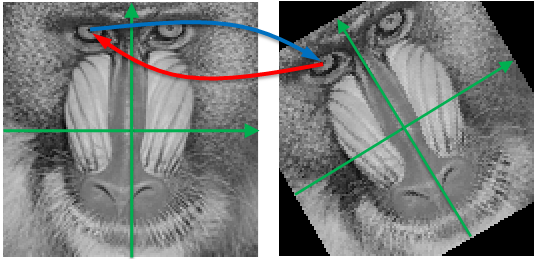
実際の変換処理は以下のように行います。
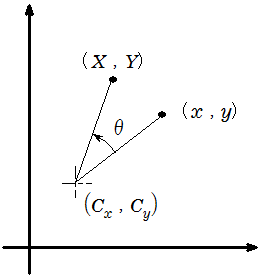
回転前の画像の座標を(x,y)、回転後の画像の座標を(X,Y)、画像の中心座標を(Cx,Cy)とすると単純に画像の中心周りに座標を回転すると以下のような行列で表されます。

この行列を回転前の画像の座標(x、y)に関して解けばいいので、行列の式の両辺にそれぞれ逆行列をかければいいので、以下のような手順で行列を解いていきます。

これで、回転前の座標(x、y)に関して解くことができます。
でも、逆行列を解くのは面倒と思う事なかれ。
(+Cx,+Cy)の平行移動の逆行列は(-Cx、-Cy)方向への移動と同じ、+θ方向への回転の逆行列は-θ方向への回転と同じなので、
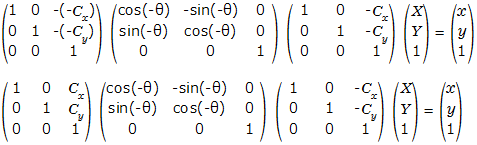
とすれば、逆行列を解くことなく回転後の座標(x、y)に関して座標を解くことができます。
このようにして画像の回転処理を行うと、このようになります。
 |
→ |  |
| 回転前の画像 | 回転後の画像 |
でも、回転後の画像はなんかギザギザしてしまっていますが、これは回転前の画像の座標を計算するとほとんどの場合、画素の画素の間の座標となってしまいますが、上図の例ではこの座標を四捨五入して輝度値を参照しているためで、bilinearやbicubicなどの補間を使うと少しは滑らかな画像となります。
今回は画像の回転について紹介していますが、画像の拡大縮小についても同様の考え方で処理することができます。
関連記事
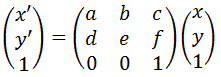

コメント