こちらのページでは、フーリエ変換のイメージをビジュアル的に見せるためのプログラムになります。
単に、フーリエ変換をしたい場合は、下記のプログラムをご使用下さい。
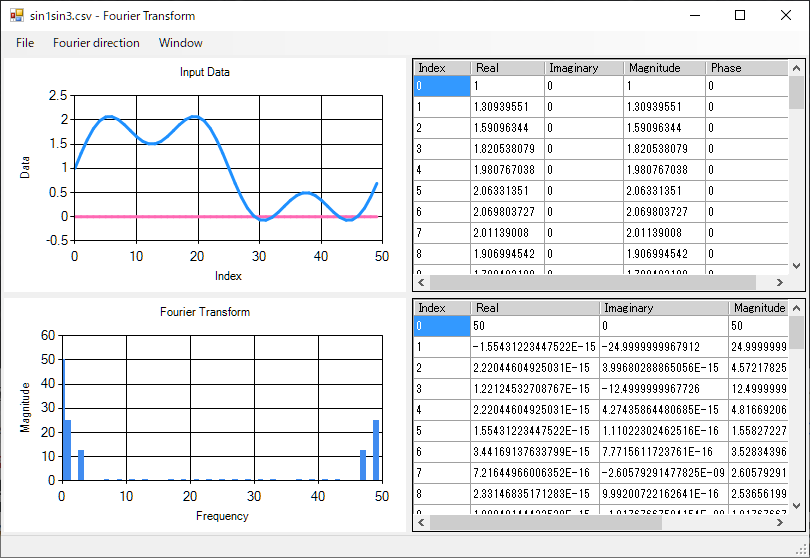
フーリエ変換を教える時に、自分の中では糸(データ)を巻き取るようなイメージ↓(こんな感じ)

があるのですが、これを分かるように説明するのがなかなか難しく、その様子が分かるように、C#でプログラムを作成してみました。
動いている様子はこちら↓
実際のプログラムはこちら↓(.NET Framework4.5.2以上で動作すると思います)
上記ファイルを解凍後、FourierTransformAnimation.exeファイルをダブルクリックすると、プログラムが実行できますが、Windowsの警告画面が表示されるので、「詳細情報」をクリック後、プログラムを実行してください。
また、いくつかサンプルデータを入れてありますので、sampledataフォルダ内のcsvファイルを開いてお試しください。
フーリエ変換で用いている式は、いくつかあろうかと思いますが、下記の式に基づいて処理を行っています。
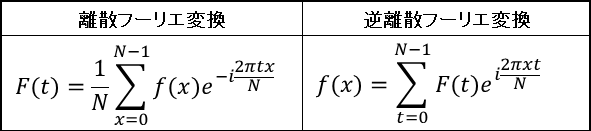
基本的な機能としては
●CSVファイルによる任意データ入力
●データの離散フーリエ変換
●離散フーリエ変~逆離散フーリエ変換までを動画表示
●窓関数
●離散フーリエ変換の結果をファイル保存
となります。
プログラムの説明
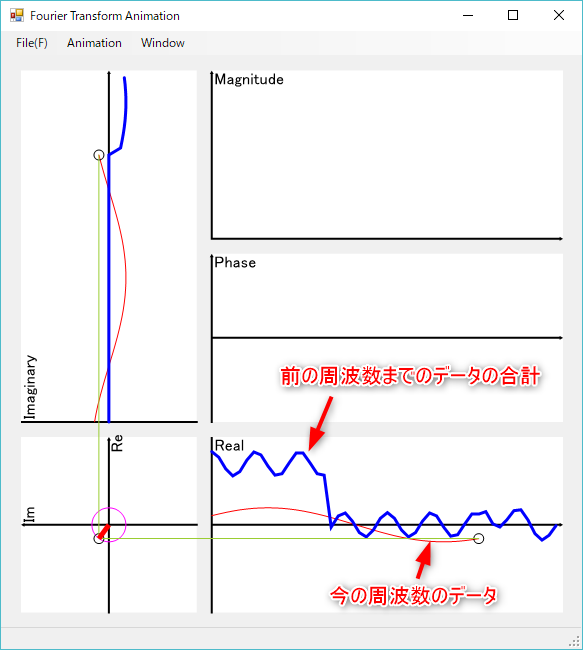
データファイルを開くと、離散フーリエ変換を行い、大きさと位相を表示します。
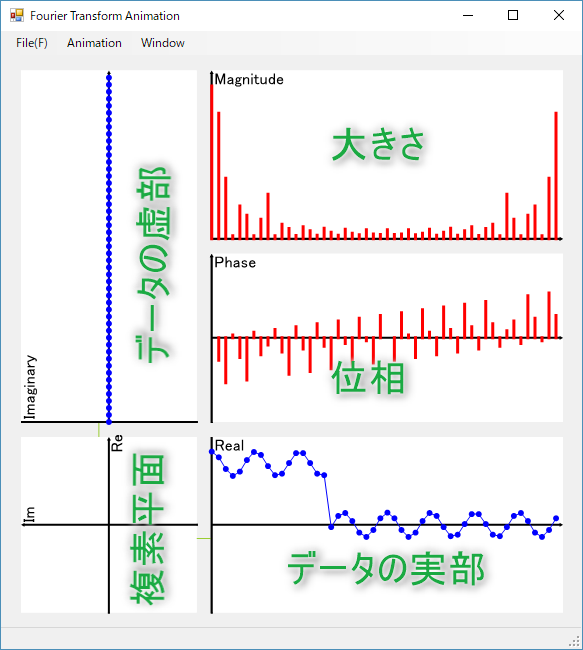
処理のアニメーションの時に用いる複素平面のグラフは、90°反時計周りに回転した状態が初期状態になっています。
離散フーリエ変換の途中途中に出てくる赤い線は、複素平面において、原点からデータの平均の位置までの線で、この線の大きさをMagnitudeグラフへ記載しています。(描画スケールが異なります。)
さらにこの線の傾き(12時方向が0°で反時計周りが正)をPhaseグラフへ記載しています。
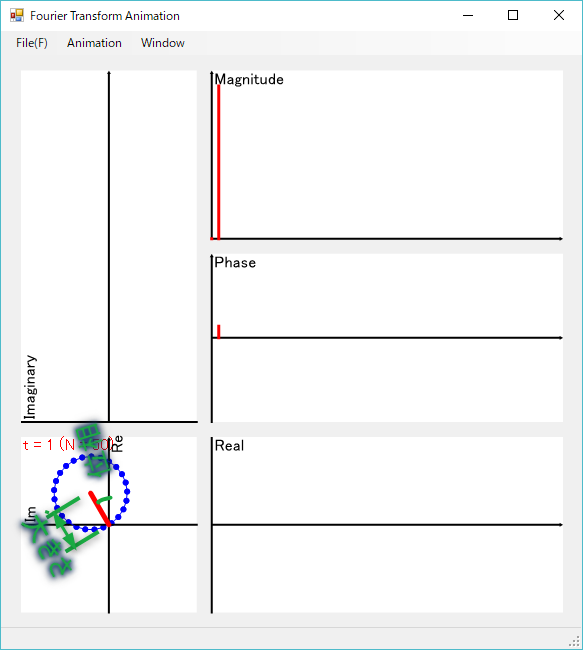
逆離散フーリエ変換の時は、各周波数のデータを積算していきますが、前回までのデータの合計を太い青い線で、現在の周波数のデータを赤い線で表示しています。
使用方法
ファイルを開く
ファイルメニューより、File → Open(*.csv) をクリックし、CSVファイルを選択します。
CSVファイルのフォーマットは1行に1データを縦に記載します。
【例】
1.2
1.107165359
0.914844142
0.80157706
0.872515202
1.061803399
1.193716632
1.145793725
0.962523737
0.814044703
0.838196601
1.012558104
1.175261336
入力データに虚数成分がある場合は、実数と虚数をカンマ(,)でつなげて以下のようにします。
【例】
1,0
0.999390827,0.034899497
0.99756405,0.069756474
0.994521895,0.104528463
0.990268069,0.139173101
0.984807753,0.173648178
0.978147601,0.207911691
0.970295726,0.241921896
0.961261696,0.275637356
0.951056516,0.309016994
0.939692621,0.342020143
0.927183855,0.374606593
0.913545458,0.406736643
0.898794046,0.438371147
0.882947593,0.469471563
データ数がどこまでいけるか?評価していませんが、アニメーション表示をするなら50~100個ぐらいまでが目安です。
アニメーション表示しなければ、そこそこいける?!
アニメーションの開始/停止
Youtubeの動画のように、処理の様子を動かすには、ファイルメニューの Animation → Start/Stop をクリックします。スペースキーを押しても同様の動きをします。
アニメーションのステップ実行
処理を1つ1つのデータで行う場合は、アニメーションを停止させ、矢印キーの右(→)を押します。
アニメーション速度の調整
アニメーション速度を速くする場合は、矢印キーの上(↑)、遅くする場合は、矢印キーの下(↓)を押します。
窓関数処理
基本的に全データを1周期分を想定していますが、この1周期に窓関数(Hamming、Hanning、Blackman)を通します。
ファイルメニューの Window → Hamming、Hanning、Blackman をクリックします。
フーリエ変換のイメージ
フーリエ変換では、データを複素平面へ巻き取るようなイメージでになります。
試しにCosθのデータ全体を1回転で巻き取るようにすると
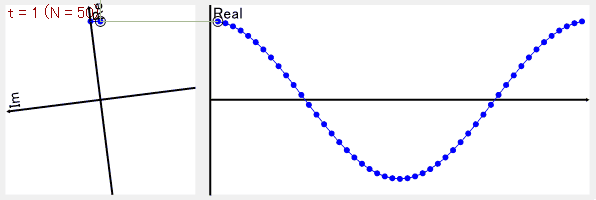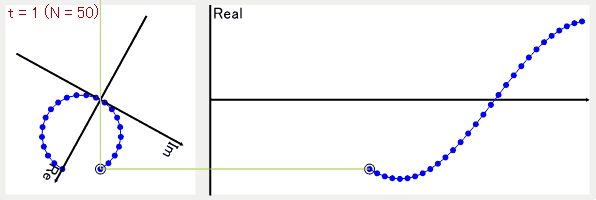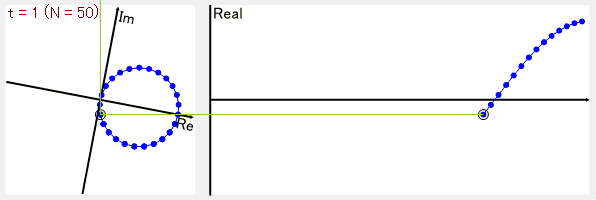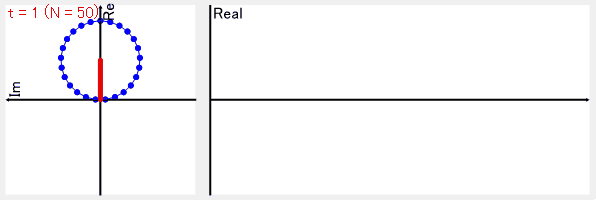
最終的に複素平面の原点から、データが巻き取られた点(複素平面上の点)の平均の位置までの線の大きさが、その周波数の大きさで、線の傾きが位相となります。
このデータを巻き取るときの回転の速度が、データ全体を0回転、1回転、2回転・・・で巻き取るようにすると、それぞれの周波数(0,1,2・・・)の大きさと位相が取得できます。
試しにCosθのデータ全体を2回転で巻き取るようにしてみると、複素平面上の点の平均は0となります。
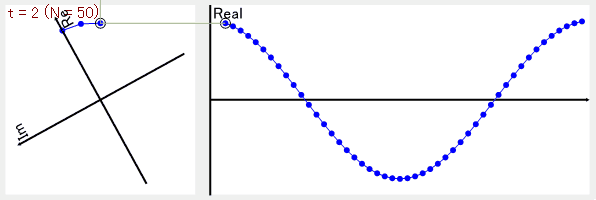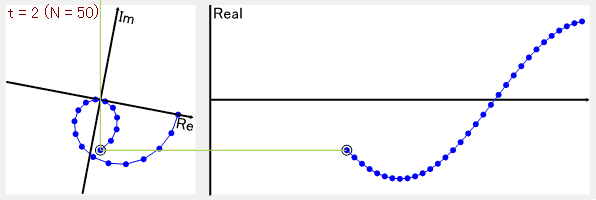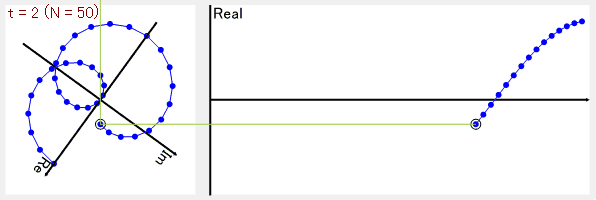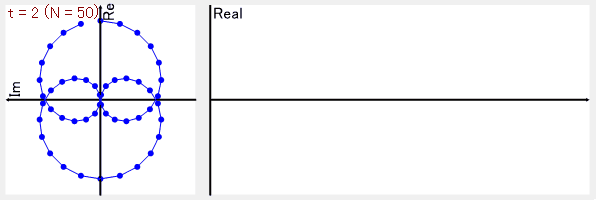
もともとのデータにない周波数成分(Cos2θの成分)は、複素平面上で平均を取ると、データが相殺されて0になるのが面白い!
逆変換の場合は、取得した各周波数ごとの大きさと位相からコサイン波形を生成し、足し合わせた結果が変換後の実部となります。
ここで、ちょっと違和感があるであろう コサイン波形 と書きましたが、サイン波形を足し合わせた結果は、虚部となります。
おそらくこんな書き方をする人はいないのですが、データの個数をN、周波数tの時の大きさをAt、位相をφtとすると、逆変換後の実部(Re)と虚部(Im)は以下のようになります。
$$Re(x)\quad =\quad \sum _{ t=0 }^{ N-1 }{ { A }_{ t }Cos(\frac { 2\pi t }{ N } x+{ \varphi }_{ t }) } \\ Im(x)\quad =\quad \sum _{ t=0 }^{ N-1 }{ { A }_{ t }Sin(\frac { 2\pi t }{ N } x+{ \varphi }_{ t }) } $$
以下の画像は周波数1の結果を逆変換したものになります。
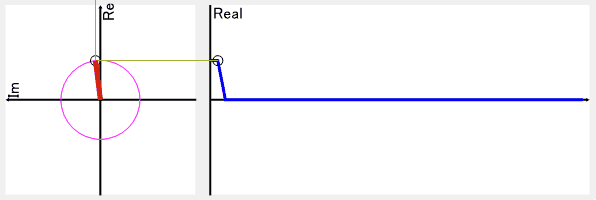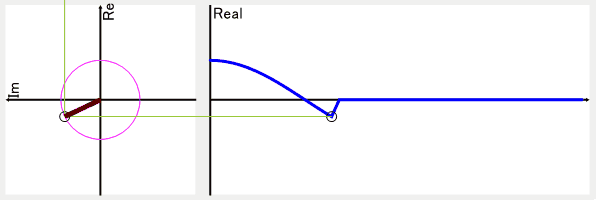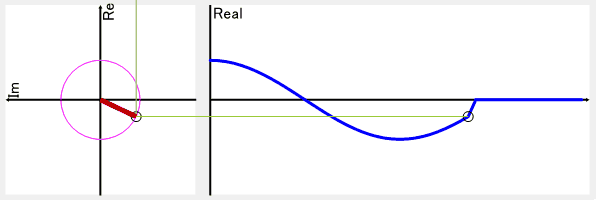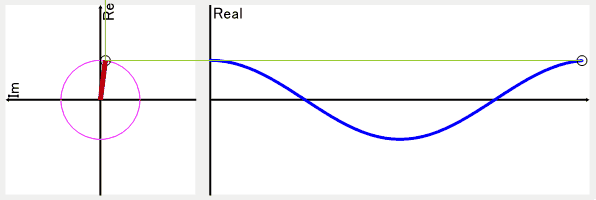
これだけを見ると、実部のグラフのcosθの振幅は小さくない?!
と思われたかもしれませんが、フーリエ変換を行う元々のデータに虚数部分が含まれない場合、大きさが同じで位相がマイナスの関係になった周波数が存在します。
こんな感じ↓
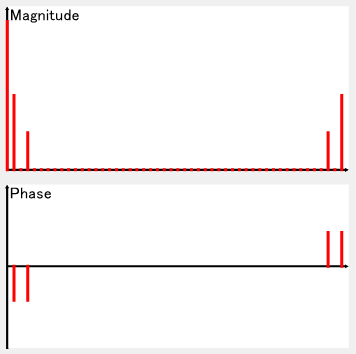
この2つの波形を足し合わせる事で、逆変換では元の波形に戻ります。
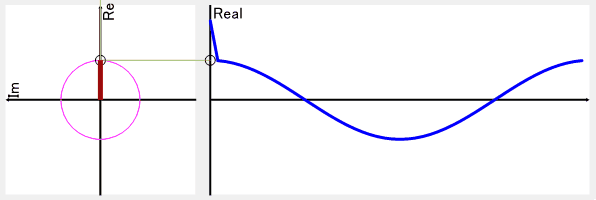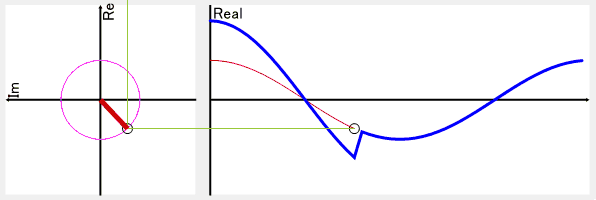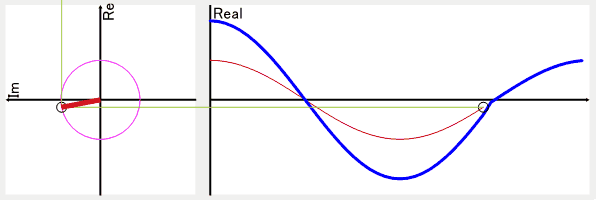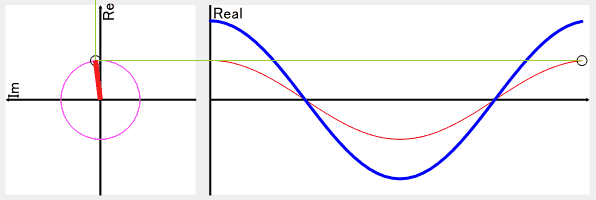
この部分の詳細を知りたい場合は、複素共役で調べてもらうと分かるかも?しれません。
このフーリエ変換を発明したジョゼフ・フーリエさんは、自分自身をミイラのように包帯でグルグル巻きになるという、ちょっと変わった趣味の持ち主だったそうですが、このグルグル巻きになった時にフーリエ変換が思いついたのではないのかな?(詳細は不明)
←フーリエ変換へ戻る



コメント