複素数のイメージ

離散フーリエ変換を勉強すると、突然

e^iθ = cosθ + i sinθ

みたいな式が突然出てきて、これが何だかよく分からないまま、とりあえず公式だけを覚えてみたり．．．

しかも　i 　は「実際には存在しない虚数」みたいに教わったので、存在しない物は、なかなかイメージもしにくい。

で、いろいろ調べてみて、今ではなんとなく

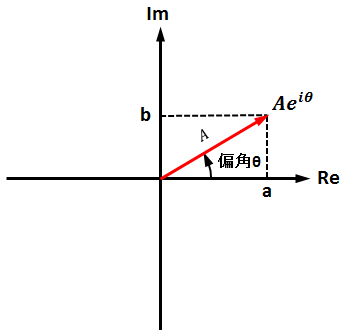
e^iθ　は複素平面における　長さ１、傾きθ　のベクトル

ぐらいの認識でいます。

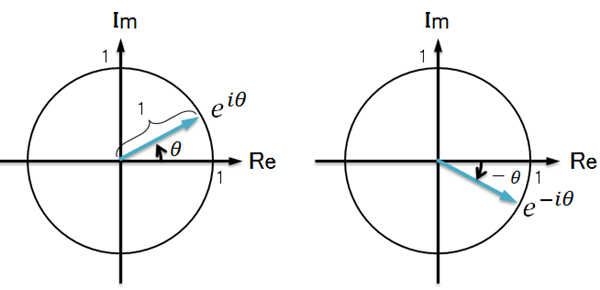
複素平面ではX軸に相当する部分が実部（Real part）、Y軸に相当する部分が虚部（Imaginary part）と呼ばれます。

回転方向は反時計まわりが正で時計まわりが負となります。

よく　e^-iθ　というのも目にしますが、これはむしろ　e^i(-θ)　と　書いてくれた方が分かりやすいと思いますが、e^-iθは、回転方向がマイナス、つまり時計まわりになります。

また、e^iθ　の頭に係数が付く場合がありますが、その係数分だけベクトルの長さが変化します。

例えば　2e^iθ の場合だと

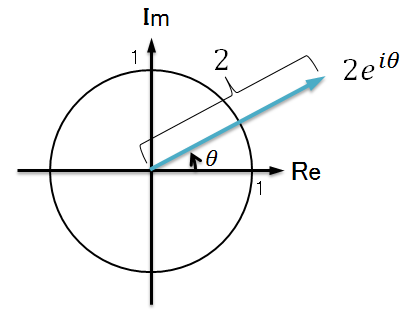
のようにベクトルの長さが２となります。

係数の値が負の場合は、ベクトルの向きが逆になり、-2e^iθ の場合だと

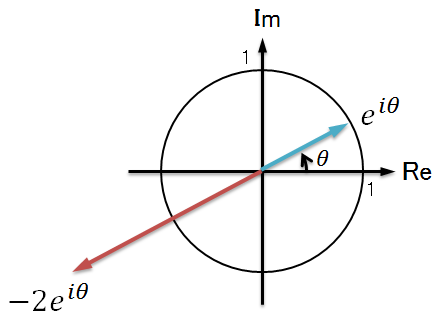
のようになります。

ただ、実際には　e^iθ　の頭に係数はθの値に応じて変化する場合が多く、例えば

(sinθ) e ^iθ

のθの値を0～360°で変化させるとどうなるか？というと、このよう↓になります。

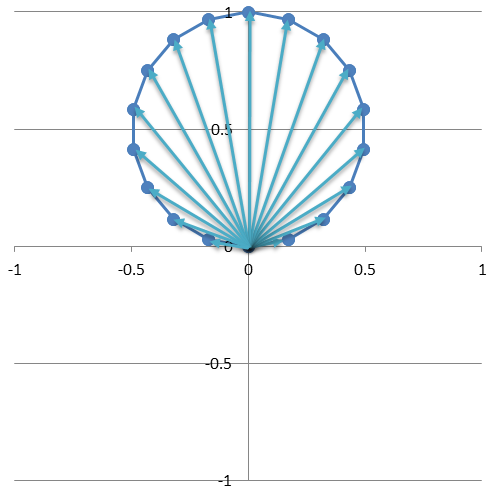
実はフーリエ変換をイメージで覚えるうえで、上図のように思えた事が最大のポイントで、とても嬉しかった～！！！

上図をよ～く見てみると、ベクトルの先端は円を描き、この円の中心が（0, 0.5）の座標になっています。

これを少し言い方を変えると、円の中心へのベクトルは長さ０．５、傾きが＋９０の位置にあります。

この事は、すでに少しだけフーリエ変換になってます。

と、ここまで説明しといて、例題としては　 (sinθ) e ^-iθ の方が良かったかな．．．ちょっと失敗？？

ちなみに(sinθ) e ^-iθ だと、円の中心は（0, -0.5）の位置に来ます。

複素数、複素関数について、もう少し詳しく知りたい方は、下記ファイルが参考になると思います。

複素関数を学ぶ人のために

関連記事