フーリエ変換とは？

フーリエ変換は何をしているのか？？？

下図の示すように、任意波形を各周波数の成分に分解し、その大きさ（振幅）および位置（位相）を求める計算がフーリエ変換となります。

逆に、振幅と位相から元の波形を求める計算が逆フーリエ変換となります。

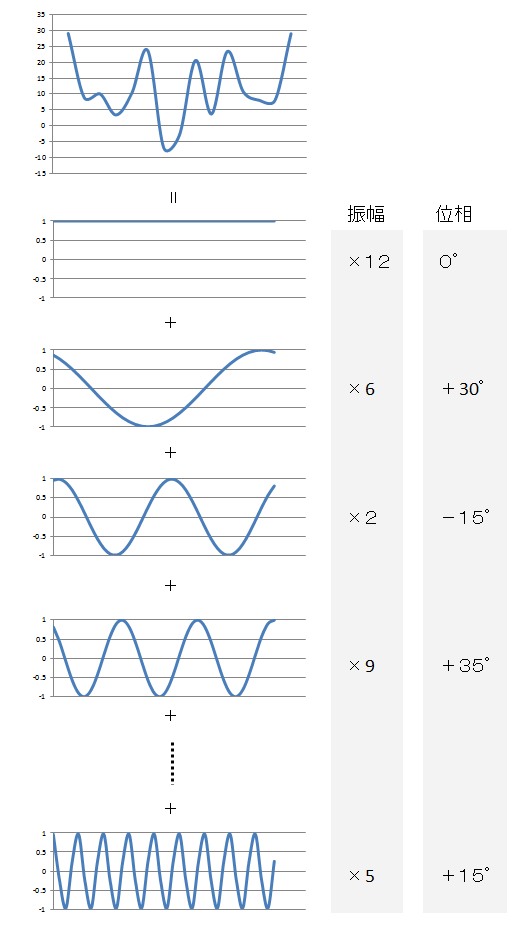
このフーリエ変換を行うと何が良いのか？？？

用途は様々なのですが、

などなど。

ここで、私がなかなかフーリエ変換を理解できなかったポイントですが、

「任意波形はサイン波形を足し合わせると求める事ができる！」

みたいな説明が良くあります。さらに位相についても触れられていない場合が多いです。

しかし、この説明だとsin(0°)は、いつも０（ゼロ）なので、いくら各周波数成分を足し合わせても０°の値は０になってしまいます。

そのため、sin波形で考えるのではなく、cos波形で考えた方が良いと思います。

この時、各周波数の成分は下記の式で表されます。

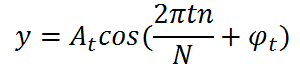
ただし、

Ｎ：データ個数

t = ０、１、２、・・・・Ｎ－１

n = ０、１、２、・・・・Ｎ－１

Ａt：tの時の振幅

φt：tの時の位相

t：データ全体に含まれる１周期分の波の個数。この値で周波数を調整します。

また、一度は聞いた事があるであろうパワースペクトルの値は振幅そのものを求めていない場合が多い。

（この事にはついては、別の記事で説明したいと思います。）

画像処理をやった事がある人では、フーリエ変換は、各周波数をテンプレートとしたテンプレートマッチングを行い、相関値がフーリエ変換のパワースペクトルに相当していると思えば、感覚的には似ています。

（ただし、数学的には異なります。）

と、ざっくりなイメージはこんな感じです。

もう少し、まじめにフーリエ変換を理解したい場合は内積や正規直交規定を理解しておくと、良いかと思います。