ここではExcelの標準の機能であるフーリエ解析について紹介したいと思います。
フーリエ変換は、ざっくり言うと信号の中から各周波数ごとの大きさと位相を求める変換です。
この”信号”と言っている部分が音や画像のような測定データの場合、この”信号(データ)”に対してフーリエ変換を行うのが離散フーリエ変換となります。
しかし、離散フーリエ変換は処理速度が遅いので、離散フーリエ変換を行うんだけど、データ個数を2のn乗(2, 4, 8, 16, 32・・・)個に制限することで、高速に処理することができる処理アルゴリズムが高速フーリエ変換[Fast Fourier Transform(FFT)]となります。
ここで、フーリエ変換の公式ですが、主に以下の3つの公式があります。下図の公式を見て頂くと分かりますが、異なるのはシグマの頭についているデータ個数Nに関する係数のみ異なります。
いくつも公式があるのは、おそらくプログラム的な都合で、
1番目の公式が本来の公式?
2番目の公式は、フーリエ変換では各周波数の大きさが相対的にどの周波数が大きいのか?を解析的に用いる場合が多く、離散フーリエ変換しかしない(逆変換をしない)場合も多いので、1/Nの計算を省き処理を軽くしたかった?エクセルでは、この2番目の公式を用いています。
3番目の公式は離散フーリエ変換と逆離散フーリエ変換のプログラムをできるだけ共通にしたかったため?異なるのは e の乗数の符号のみとなります。

N : データ個数
t: 全データに含まれる波の個数(何周期分か?)
x : データのインデックス番号 x = 0, 1, 2,… , N-1
データの準備
エクセルのフーリエ解析はFFTなので、データの個数は2のn乗個(2, 4, 8, 16, 32, 64・・・)に限られ、最大4096個まで処理が可能です。
今回はデータの個数は32個用意しました。
実際にフーリエ解析したいデータは各自、用意してください。
データはどこかに1列に書いておけば大丈夫です。(あとで、データの場所を指定します)
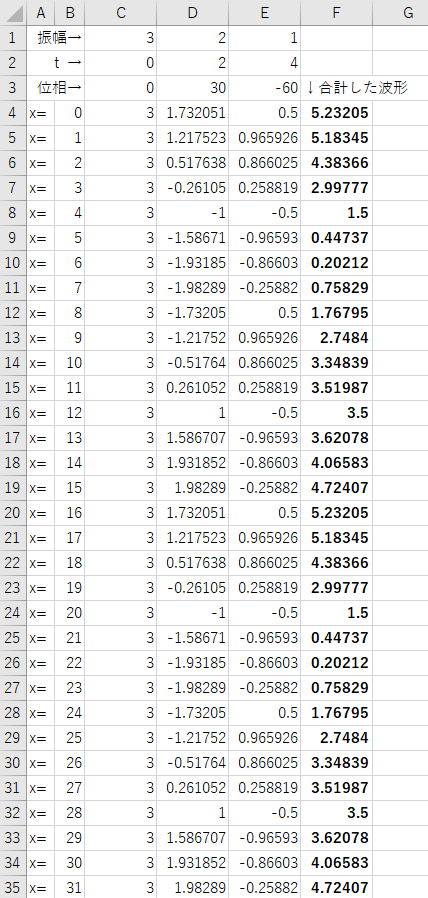
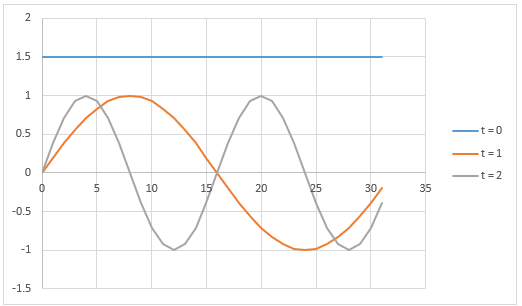
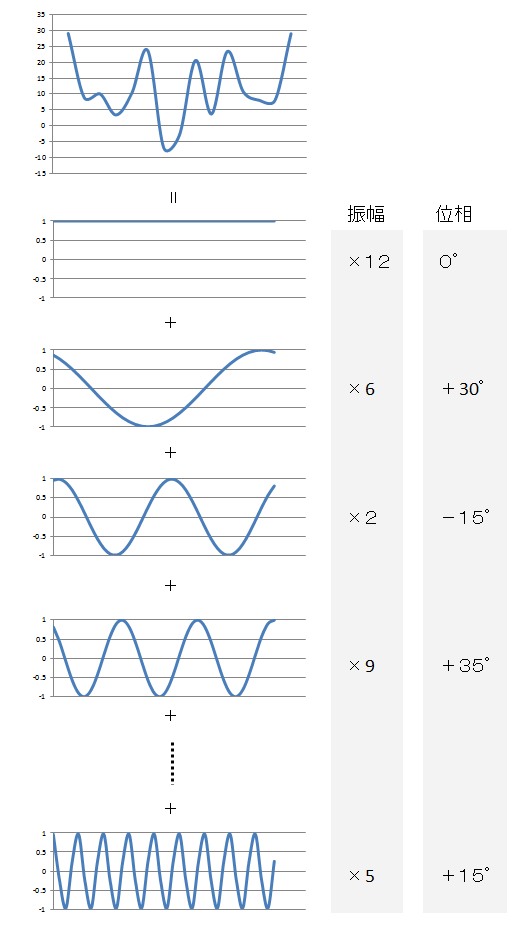
結果が分かりやすくなるように、
全く振動していない(t=0)データ(値=3)と、
2周期分(t=2)のデータ(振幅=2、位相=30°)と、
4周期分(t=4)のデータ(振幅=1、位相=-60°)
の3つの波形を合計したデータに対してフーリエ変換を行います。
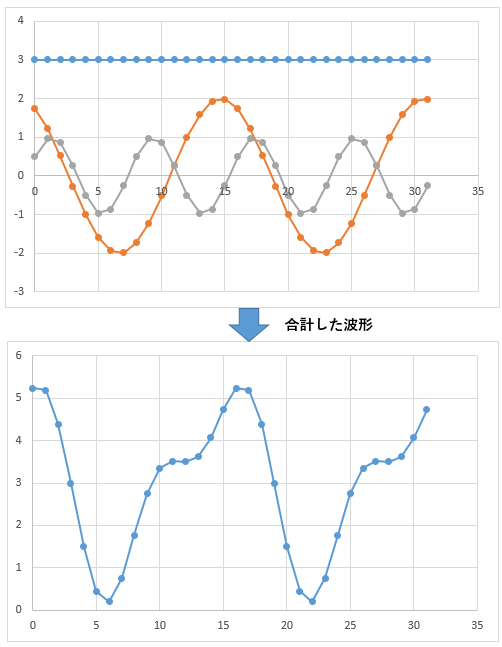
Excelでフーリエ解析の手順
Excelでフーリエ解析を行うには分析ツールというのを表示する必要があります。
この分析ツールの表示方法は下記のページを参照下さい。
メニューのデータ→データ分析を選択します。
※ホーム→データ分析にあるデータ分析とは別なので注意してください。

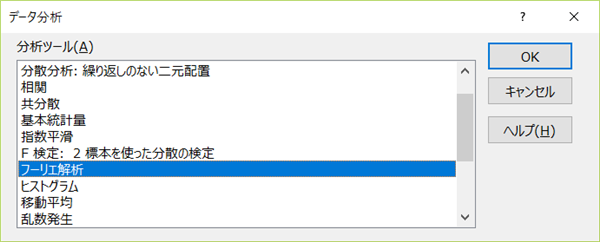
表示されたウィンドウからフーリエ解析を選択しOKを押します。
表示されたウィンドウの入力範囲の部分にある上矢印の部分をクリックします。
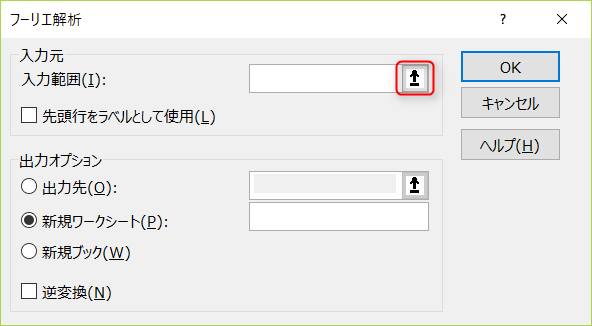
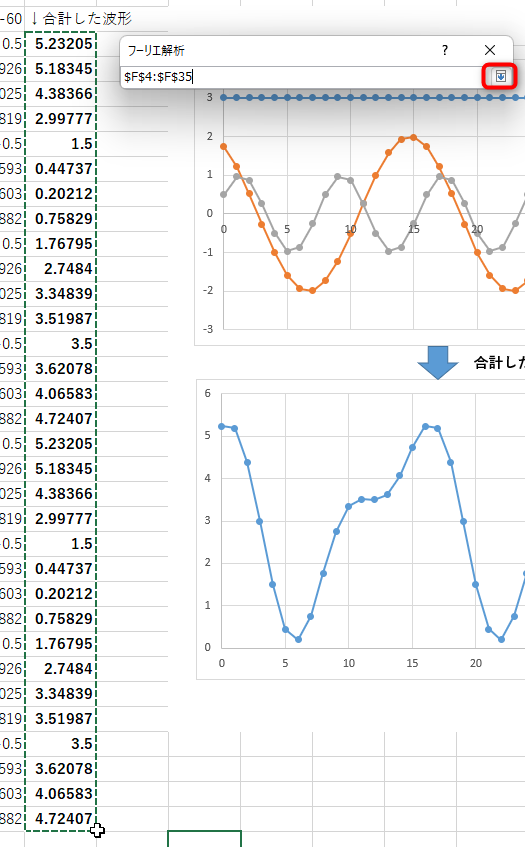
この状態で、フーリエ解析を行うデータを選択(2のn乗個の最大4096個まで)し、それでよければ下矢印をクリックします。
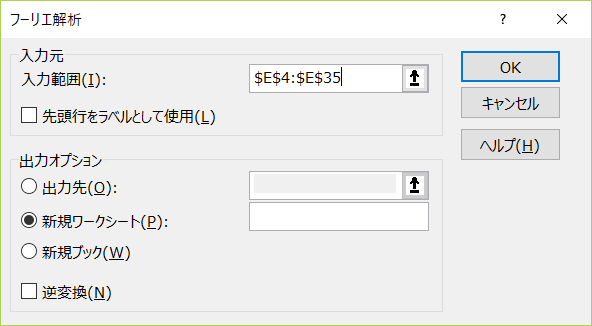
フーリエ解析の結果の出力先はいくつか選べるのですが、今回は新規ワークシートにするとして、OKボタンをクリックします。
そしてこれ↓がフーリエ変換された結果です。
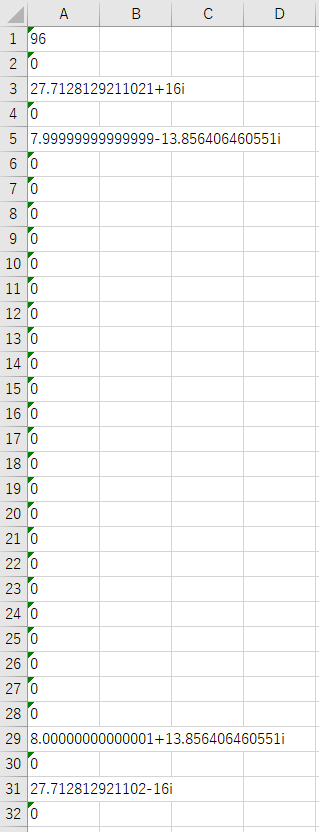
フーリエ変換の結果の見方
※ここから先は、入力データが実数(虚数成分が無い)の場合を前提として説明します。
フーリエ変換の結果は
96
0
27.7128129211021+16i
0
7.99999999999999-13.856406460551i
0
0
:
のように複素数(実数と虚数成分が含まれる)が並んでいますが、これは上から順にt=0、1、2、…の時の結果になっています。
tの値は、FFTに用いたデータ全体に何周期分の波が含まれているか?を表しています。
tの値から周波数f(Hz)を求めるには、データ全体のサンプリング時間をΔt(sec)とすると、周波数は
$$f=\frac{t}{\triangle t} (Hz)$$
となります。
ここで、フーリエ変換の結果に、tの値と周波数fを書き加えます。
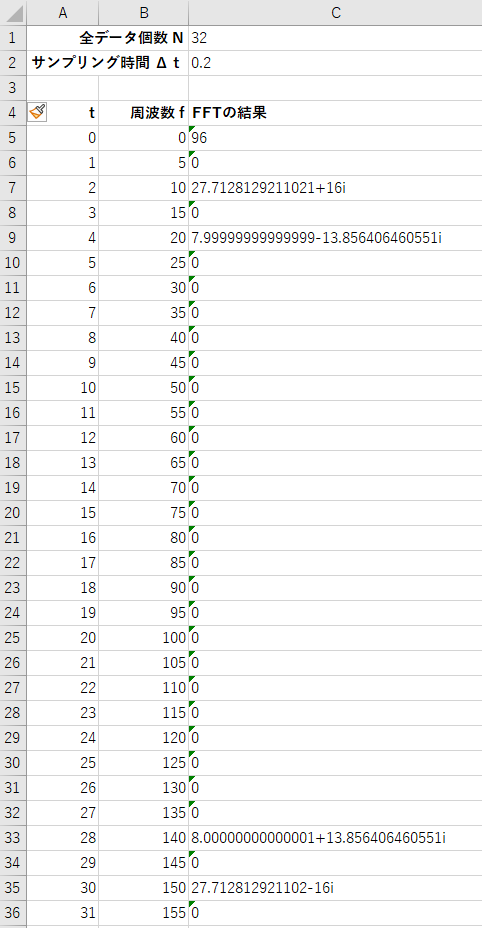
この結果を見ると、多少の計算誤差はありますが、 t= 2 と t = 30、 t = 4 と t = 28 の値が、虚数成分(i の係数)の正負が異なるだけで、似ている事がわかります。
この実数は同じで虚数の正負が異なる値を複素共役と言います。
フーリエ変換の入力データが実数の場合、必ずこのようになるのですが、t と N – t が共役となるため、フーリエ変換では、 t = 0~N/2 までの結果のみを使う場合がよくあります。
フーリエ変換の結果から各周波数の振幅Aを求めるには、フーリエ変換の結果(複素数[実数と虚数])の大きさ |F(t)| を用いると
t = 0 と t = N/2のとき
$$A=|F(t)| / N$$
t = 1 ~ N/2-1 のとき
$$A=|F(t)| / N \times 2$$
となります。
エクセルで複素数の大きさを求めるには IMABS()関数 を用います。
さらに複素数の偏角(位相)を求めるには IMARGUMENT()関数 を用いますが、偏角の結果はラジアン単位なので、度の単位に変換するには DEGREES()関数 を用います。
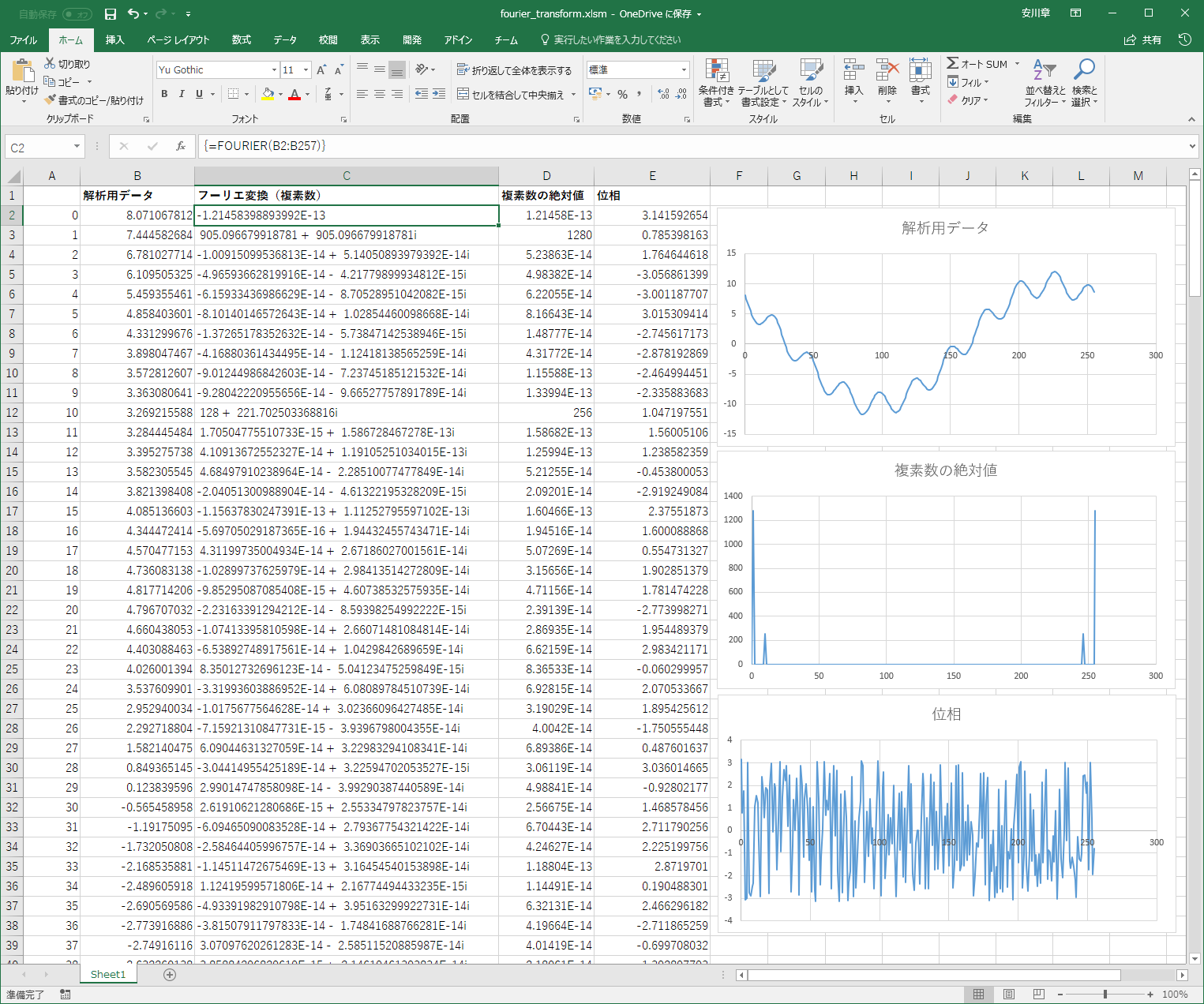
これらの事をエクセルの結果に複素数の大きさ、各周波数ごとの振幅および位相を追加すると以下のようになります。
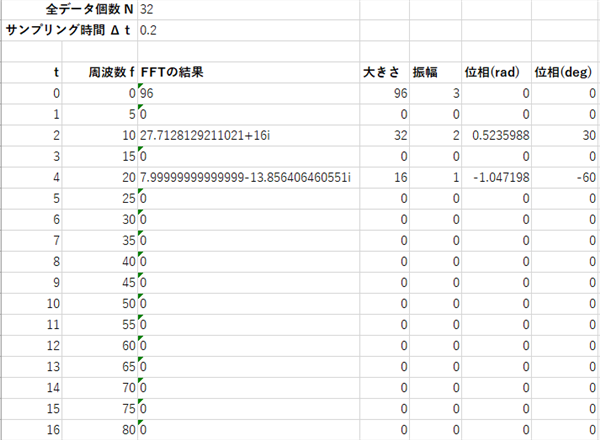
これで、データをFFTして、各周波数ごとの振幅(A)と位相(φ)を求める事ができています。
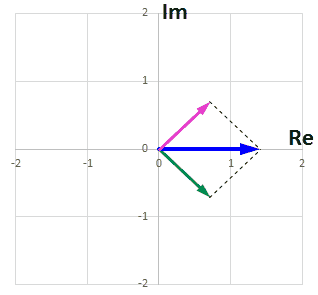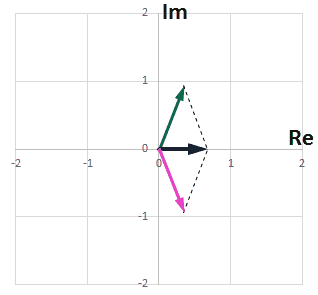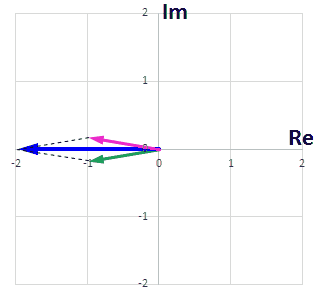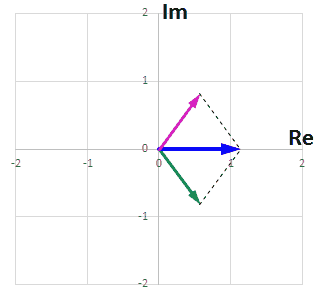
各周波数ごと(各tごと)の波形は
$$A_{t} \cos(2\pi t\frac{x}{N}+\phi_{t})$$
となります。
今回のFFT解析に用いたExcelファイル(*.xlsx)は、下記リンクをクリックしてダウンロードできます。
パワースペクトルは??
FFT解析は、各周波数のパワースペクトルを求めること!
みたいな認識もあるかと思いますが、ここまでの説明にパワースペクトルが出てきていません。
パワースペクトルは、FFTで求めた各周波数の結果(複素数)の大きさを振幅スペクトルと言い、振幅スペクトルを2乗したものをパワースペクトルと言います。
パワーという響きから、どうしても力?みたいなのをイメージしてしまいますが、どちらかというと、C言語でn乗の計算をするときに pow関数 を用いると思いますが、このn乗の方に近いでしょうか?(本当のところはよく知りません。。)
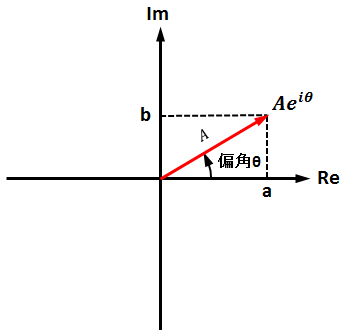
各周波数ごとに求められたFFTの結果(複素数)を a + bi とすると
$$振幅スペクトル=\sqrt{a^{2}+b^{2}}$$
$$パワーペクトル=(振幅スペクトル)^{2}=a^{2}+b^{2}$$
となることから、プログラム的にはパワースペクトルの計算の方がルートの計算をしていない分だけ計算コストが低くなります。
エクセルでは、IMABS()関数で振幅スペクトルを求め、振幅スペクトルを2乗(^2)することで、パワースペクトルを求める事になり、計算コストが増えてしまい、ちょっと微妙。。
複素共役の性質
入力データが実数のときのFFTの結果で t と N – t が共役になると説明しましたが、
複素数 a + bi と、共役の複素数 a – bi と足し合わせると
$$(a+bi)+(a-bi) = 2a$$
となるので、虚数成分は打ち消しあい、実数成分が2倍となります。
この性質から、振幅を求める際に、t = 1 ~ N/2-1 のとき、最後に x 2 を付けているのは、そのためです。
←フーリエ変換へ戻る
参考




コメント
私の説明が不十分でした。
本文全体で「パワースペクトル」と書かれている部分を全部修正した方がいいです。
「パワースペクトル」→「振幅」
とすべきところと、
「パワースペクトル」→「スペクトル」
とあります。
ついでですが、折れ線グラフ、棒グラフの縦軸は「振幅」ですね。
小久保様、コメントありがとうございます。
ただ、私の理解が付いていけない部分がありまして。。
ここでの記事ではデータ個数が32個で周波数を0~16まで変えた例で示していますが、17~31の成分(ここでパワースペクトルと言っている成分)も出てきます。
入力データが実数の時は、複素共役となる2つの周波数成分を足した時に振幅となりますが、各周波数の成分0~31全てを「振幅」と表現するのには、少し抵抗があるのですが、合っていますでしょうか?
また、Excelのフーリエ解析で出てくる値は、本記事で最初の方に示した2番目の式が用いられているのですが、フーリエ変換(順変換)の時にはデータの個数で割られないので、やっぱり「振幅」と書くのには抵抗があるもので。。
(だからと言って、何と言った方が正解かも分かっていないのですが。)
とても参考になりました。ありがとうございます。
ただ、気になる表現があったのでコメントさせていただきます。
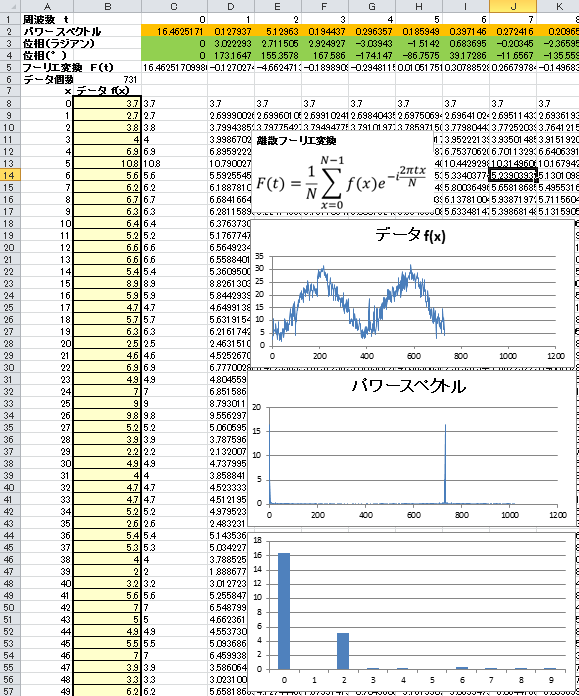
最後の示された図ですが、フーリエ変換で直接出てくるのは振幅であり、それをパワースペクトルと呼ぶのは適切でないと思います。
単にスペクトルと言えばいいのでは?
なお、波のエネルギー(パワー)は振幅の2乗に比例するので、振幅(imabs)の2乗を算出し、さらに複素共役分のパワーを足し合わせればパワースペクトルになります。
最後の図の例をパワースペクトルで表すと、周波数0の成分は1、その他の成分は0.5になります。
小久保様、ご指摘ありがとうございます。
とりあえず、最後の図に関する「パワースペクトル」の部分を修正しましたが、これで合っていますでしょうか?
私の記事では、数学的な理解の部分は、自己流なところもあって、学術的にはかなり怪しいかと思います。。