画像の拡大縮小、回転、平行移動などを行列を使って座標を変換する事をアフィン変換と呼びます。
X,Y座標の二次元データをアフィン変換するには、変換前の座標を(x, y)、変換後の座標を(x’,y’)とすると回転や拡大縮小用の2行2列の行列と、平行移動用に2行1列の行列を使って
$$\left(\begin{array}{c}x^{‘}\\ y^{‘}\end{array}\right)=
\left(\begin{array}{c}a & b\\ c & d\end{array}\right)
\left(\begin{array}{c}x\\ y\end{array}\right)
+ \left(\begin{array}{c}T_{x}\\ T_{y}\end{array}\right)$$
のように表現される場合もありますが、回転、拡大縮小、平行移動を1つの3x3の行列にまとめて
$$\left(\begin{array}{c}x^{‘}\\ y^{‘} \\ 1\end{array}\right)=
\left(\begin{array}{c}a & b & c\\ d & e & f\\ 0 & 0 & 1\end{array}\right)
\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)$$
と3x3の行列で表現する場合もあります。
この表現を同次座標系と呼びます。
同次座標系では一見、3行目は無駄なようにも見えるのですが、この意味の無いような1行を追加する事で、平行移動も同じ行列の積で表現でき、逆行列を使う事で、アフィン変換後の座標からアフィン変換前の座標も簡単に求める事ができるようになります。
私は3行3列の行列を用いた同次座標系のアフィン変換しかしていない、というか断然おススメなので、同次座標系で説明したいと思います。
後半でアフィン変換の実用例を示しているので、その部分で、同次座標系の恩恵を感じてもらえると嬉しいです。
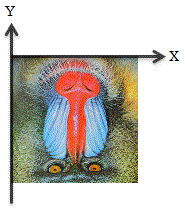
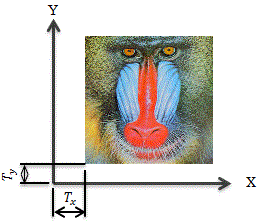
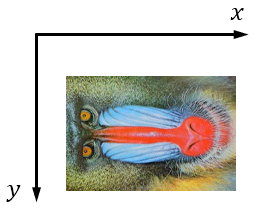
変換前の画像を以下のようにすると、
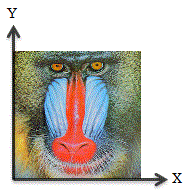
各種変換は以下の通りとなります。
拡大縮小
X軸方向の拡大率をSx、Y軸方向の拡大率をSyとすると拡大縮小のアフィン変換は
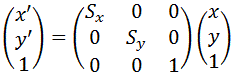
と表されます。
例)X軸方向に2倍
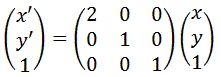

例)Y軸方向に2倍
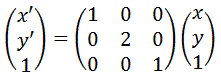

例)X軸、Y軸方向に2倍
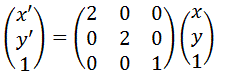

例)Y軸方向に-1倍
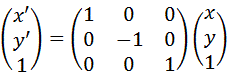
このように、ある軸(上記の例ではX軸)に対して反転する処理の事を鏡映と呼びます。
平行移動
X軸方向にTx、Y軸方向にTyだけ移動するアフィン変換は
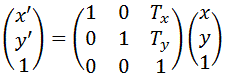
のように表されます。
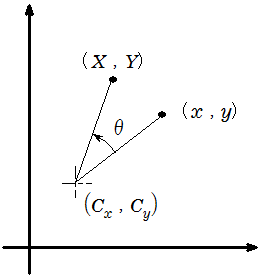
回転
原点を中心に反時計回りにθ°回転する時のアフィン変換は
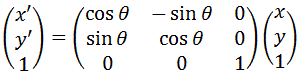
のように表されます。
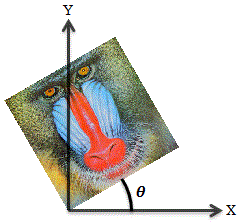
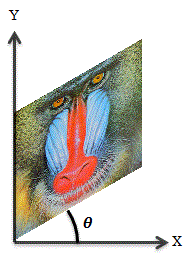
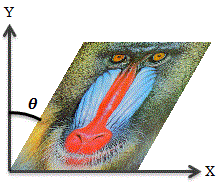
スキュー(せん断)
四角形の画像を平行四辺形に変形する処理をスキューまたはせん断といいます。
このアフィン変換は
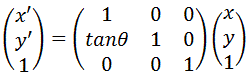
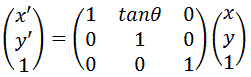
アフィン変換の実用方法
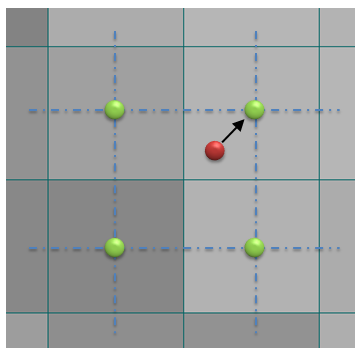
画像処理で使われるアフィン変換は、下図のようにピクチャボックスなどの左上が原点[座標が(0, 0)]で右方向が+X、下方向が+Y、時計周りが+θ方向となる場合が多いかと思います。
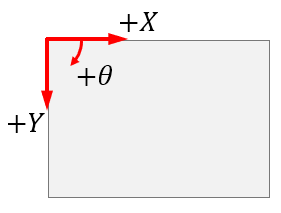
また、平行移動、拡大縮小、回転などの行列を紹介しましたが、これらの行列を1回だけで処理する事はまれで、それぞれの行列を組み合わせてアフィン変換を行います。
さらに、拡大縮小、回転、スキューのアフィン変換行列は、あくまでも原点を基点として、変換される事に注意が必要です。
例えば、画像が原点の位置に無い場合、画像をX,Y方向に2倍の大きさにしようとしたとき、単に拡大縮小のアフィン変換行列で座標を計算すると、表示位置も2倍、原点の位置から離れた位置に移動します。
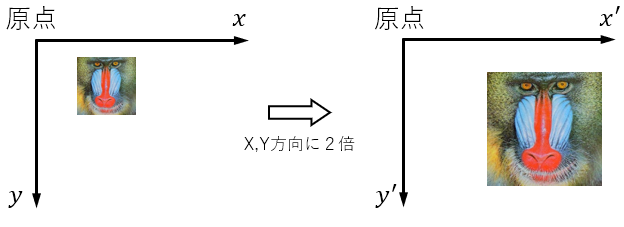
これらの事を踏まえ、画像を幅方向に2倍、高さ方向に3倍し、画像を反時計方向に90°回転、さらに、画像の左上の座標が(50, 50)から(30,180)へ移動するアフィン変換を例題にとって考えたいと思います。
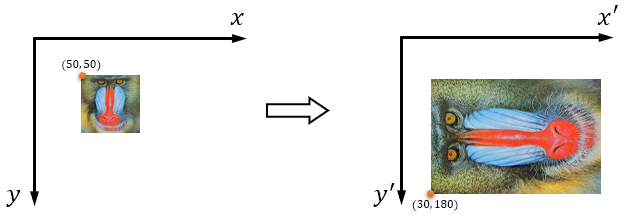
この変換は、一発で変換するアフィン変換行列を考えるのではなく、平行移動、拡大縮小、回転に分けて、アフィン変換の順番を考えます。
①拡大縮小と回転が原点を基点とするため、画像を原点の位置へ移動するため、x方向に-50、y方向に-50の平行移動します。
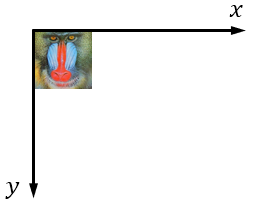
平行移動のアフィン変換行列は
$$\begin{pmatrix} 1 & 0 & -50 \\ 0 & 1 & -50 \\ 0 & 0 & 1 \end{pmatrix}$$
②拡大縮小か回転のどちらからでも構いませんが、x方向に2倍、y方向に3倍の拡大縮小を行います。
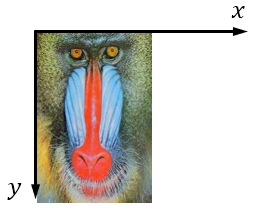
拡大縮小のアフィン変換行列は
$$\begin{pmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 1 \end{pmatrix}$$
③反時計周りに90°回転(ー90°回転)を行います。

回転のアフィン変換行列は
$$\begin{pmatrix} cos(-90) & -sin(-90) & 0 \\ sin(-90) & cos(-90) & 0 \\ 0 & 0 & 1 \end{pmatrix}$$
④最後に目的の位置へ移動するのに、x方向に+30、y方向に+180の平行移動します。
平行移動のアフィン変換行列は
$$\begin{pmatrix} 1 & 0 & 30 \\ 0 & 1 & 180 \\ 0 & 0 & 1 \end{pmatrix}$$
このようにアフィン変換を平行移動、拡大縮小、回転に分解して、変換の手順を考える事が大事です。
今回の場合は
変換前 → 平行移動 → 拡大縮小 → 回転 → 平行移動 → 変換後
としています。
画像に対してアフィン変換を行う場合、考え方としては、平行移動や拡大縮小などに分解して考えますが、画像データを毎回変換するのではなく、アフィン変換行列をまとめて計算し、一発でアフィン変換処理を行います。
具体的には、今回のアフィン変換処理を行列で表すと
$$\begin{pmatrix} { x }^{ ‘ } \\ { y }^{ ‘ } \\ 1 \end{pmatrix}=\begin{pmatrix} 1 & 0 & 30 \\ 0 & 1 & 180 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} cos(-90) & -sin(-90) & 0 \\ sin(-90) & cos(-90) & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} 1 & 0 & -50 \\ 0 & 1 & -50 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$
行列部分をまとめて計算し
$$\begin{pmatrix} { x }^{ ‘ } \\ { y }^{ ‘ } \\ 1 \end{pmatrix}=\begin{pmatrix} 0 & 3 & -120 \\ -2 & 0 & 280 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$
となり、アフィン変換行列を一発で処理する事ができます。
さらに、変換後の座標(x’, y’)から、変換前の座標(x, y)を求める場合があるのですが、その時は、行列の左側からアフィン変換行列の逆行列を掛けて、
$$\begin{pmatrix} 0 & 3 & -120 \\ -2 & 0 & 280 \\ 0 & 0 & 1 \end{pmatrix}^{ -1 }\begin{pmatrix} { x }^{ ‘ } \\ { y }^{ ‘ } \\ 1 \end{pmatrix}=\begin{pmatrix} 0 & 3 & -120 \\ -2 & 0 & 280 \\ 0 & 0 & 1 \end{pmatrix}^{ -1 }\begin{pmatrix} 0 & 3 & -120 \\ -2 & 0 & 280 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}$$
$$\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}=\begin{pmatrix} 0 & 3 & -120 \\ -2 & 0 & 280 \\ 0 & 0 & 1 \end{pmatrix}^{ -1 }\begin{pmatrix} { x }^{ ‘ } \\ { y }^{ ‘ } \\ 1 \end{pmatrix}$$
$$\begin{pmatrix} x \\ y \\ 1 \end{pmatrix}=\begin{pmatrix} 0 & -0.5 & 140 \\ 0.333 & 0 & 40 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} { x }^{ ‘ } \\ { y }^{ ‘ } \\ 1 \end{pmatrix}$$
として、変換前の座標を求める事ができます。
まとめ
- アフィン変換は平行移動、拡大縮小、回転、スキューに分けて、変換の順番を考える
- 実際のアフィン変換は、アフィン変換行列をまとめて計算し、一発で処理を行う
- 変換前の座標は逆行列を使うと、求めることができる
この順番の考え方は、ほとんどの場合、画像を原点へ平行移動し、拡大縮小、回転を行ってから、目的の位置へ移動すると、アフィン変換行列が求まりますが、他にも、特定の点を基準に拡大縮小や回転を行う場合は、その点を原点へ移動すればアフィン変換行列が求まります。
(参考)
注意点
アフィン変換では任意の3×3(2×3)の行列で表す事ができるので、任意形状に変換できそうにも思えるのですが、四角形が平行四辺形にまでは変形できるものの、台形には変形できないのでご注意願います。
この台形に変形できる処理は射影変換(ホモグラフィ)と呼びます。

アフィン変換は今回の説明のように、画像を移動、変形させるための手法として説明されますが、もう少し汎用的に座標変換として捉えると応用範囲が広がります。
例えば、データのグラフを表示する時に、横方向、縦方向に拡大/縮小した時に、表示するデータの範囲を求める場合などに応用すると、少し便利です。
関連記事
実際にOpenCVを使って行うアフィン変換については、こちらのページ↓にまとめました。

マイクロソフトの.NETやDirectXで扱うアフィン変換行列は、行と列が逆になり、行列を掛ける順番も逆(右側から掛ける)になります。
この仕様については、下記ページ↓にまとめました。


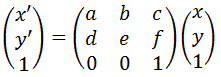



コメント
C#を勉強して半年の者です。
アフィン変換について、このサイトで勉強させていただき、感謝申し上げます。
コードをダウンロードさせていただき、
VisualStudio内でどのイベントハンドラでどういう処理を行うかについても、大変参考になりました。
ありがとうございます。
コメントありがとうございます。
アフィン変換については、拡大だけ、移動だけの説明が多いかと思いますが、「アフィン変換の実用方法」に書いてあるように、個人的には組み合わせて使う方が多いです。
また、C#だと、下記のリンクページも紹介していますが、行と列が逆で、行列を書ける順番も逆なので、注意してください。
【C#.NET】マイクロソフト仕様のアフィン変換
https://imagingsolution.net/program/csharp/microsoft-affine-transformation/#google_vignette
アフィン変換を使いこなすと、ここ↓
【C#】アフィン変換を用いて画像ビューアを作ろう!
https://imagingsolution.net/program/affine_image_transformations/
に書いてあるような事も、比較的簡単に出来ちゃいます。
「①拡大縮小と回転が原点を基点とするため、画像を原点の位置へ移動するため、x方向に-50、y方向に-50の平行移動します。」についてお聞きしたい事があるのですが、画像があらかじめ原点に合わせられていたとしても、この平行行列の式は必要ですか?
画像が原点の位置にある場合は、基本的に平行移動の部分は不要になります。
ただし、ここでは触れていないのですが、アフィン変換により画像を生成する部分を、自分で作成するのではなく、ライブラリ等の関数で行うのであれば問題になる場合があります。
「画像の原点」というのが、関数の仕様により、左上の画素の中心にあるのか、もしくは、左上の画素の左上の角が原点なる場合があります。
もし、「画像の原点」が左上の画素の中心にある場合に、画像を拡大縮小するのであれば、あらかじめ0.5画素の平行移動が必要になります。
詳細は、こちらにまとめてありますので、参考にしてください。
https://imagingsolution.net/imaging/image_magnification/
この、「画像の原点」がどこにあるのか?を調べるには、補間モードの設定がある場合には、ニアレストネイバーに設定し、最初の平行移動は行わず、拡大の倍率を10倍など、大きめの倍率で画像を拡大してみると、変な感じに画像が拡大されるので、分かると思います。
[…] アフィン変換(平行移動、拡大縮小、回転、スキュー行列)|イメージングソリューリョン […]
[…] アフィン変換(平行移動、拡大縮小、回転、スキュー行列)|イメージングソリューリョン […]
[…] アフィン変換(平行移動、拡大縮小、回転、スキュー行列)|イメージングソリューリョン […]
[…] […]
[…] […]
[…] ただ、一般的なアフィン変換では […]