.NETには標準でMatrixクラス(名前空間:System.Drawing.Drawing2D)がありますが、このクラスはアフィン変換用に作られ、3行2列の行列に限定されているため、汎用的な行列演算ができません。
汎用的な行列演算ができると、アフィン変換に限らず、射影変換や擬似逆行列を用いた近似処理も可能になります。
そこで日頃から二次元配列をそのまま行列に使えればいいのに!と思っていたのですが、PythonのOenCVっぽく簡単に?行列(二次元配列)の計算ができる.NET Framework用のImagingSolution.Matクラス(ImagingSolution.Mat.dll)を作成しました。
主な機能
行列の積・加算・減算、逆行列、転置行列、擬似逆行列、画像の読込・表示、CSVファイル保存など
ダウンロード
ライブラリ(ImagingSolution.Mat.dll)とサンプルコードは以下からダウンロードできます。
| 公開日 | バージョン | ファイル | 備考 |
| 2020.07.25 | Ver.0.1.1 | ImagingSolution.Mat_V011.zip | 暫定版 |
※ご自由に使用して頂いて構いませんが、使用は自己責任でお願いします。
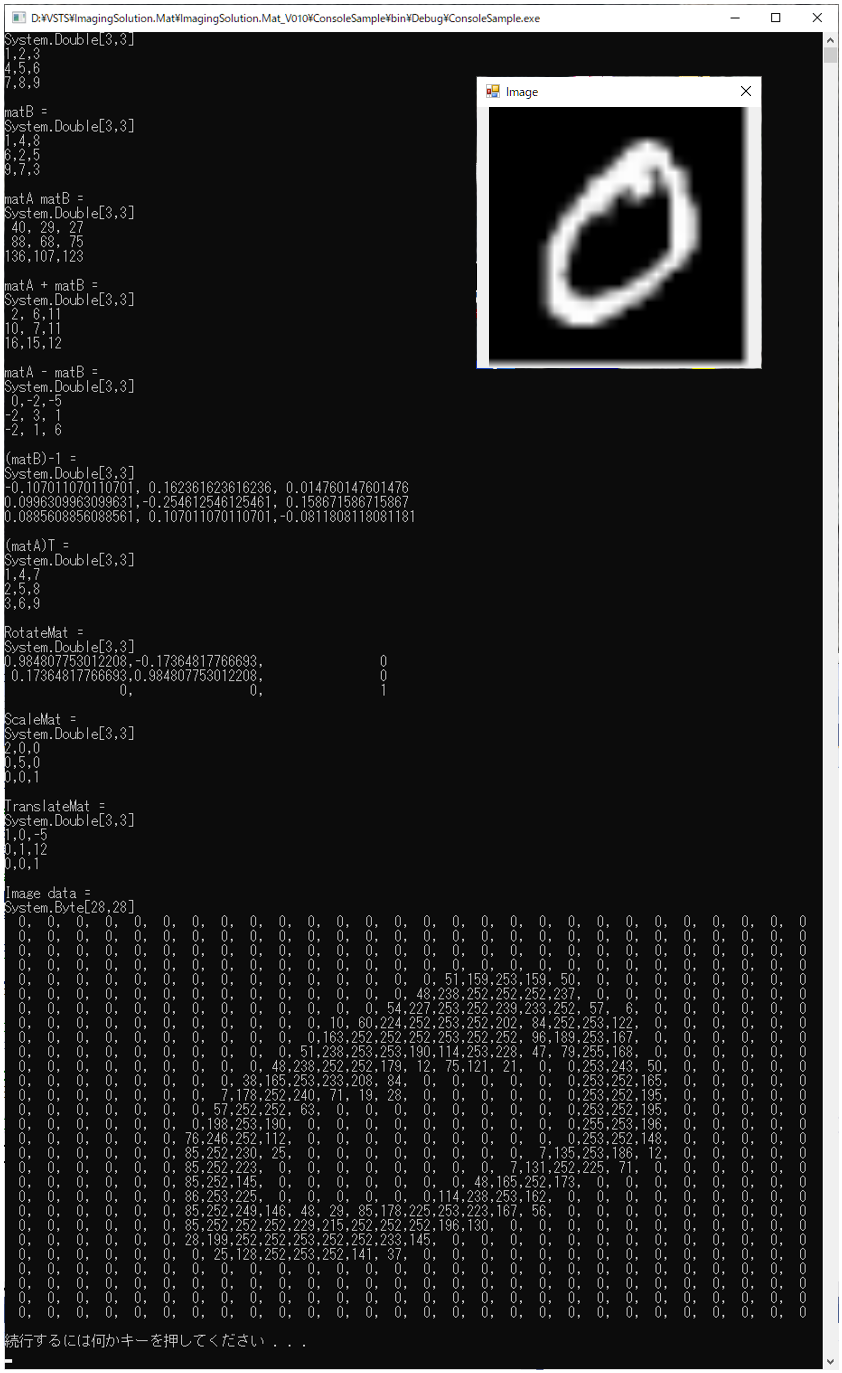
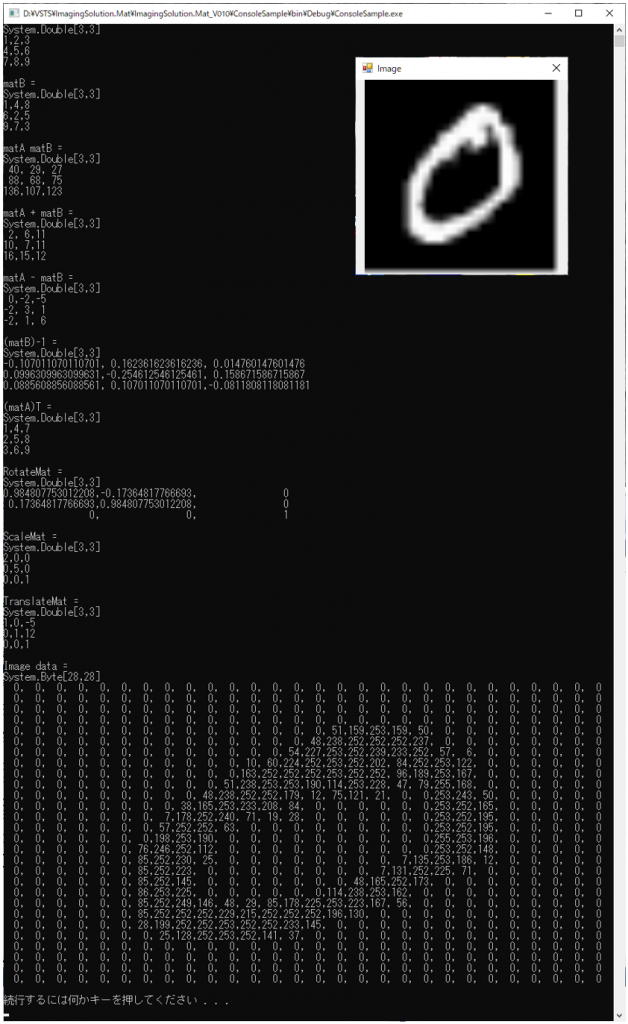
動作イメージ
サンプルコード
// 行列(matA)の設定(二次元配列で行列を設定)
var matA = new double[,] {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 }
};
matA.Print("matA ="); // コンソールへ行列の表示
// 行列(matB)の設定
var matB = new double[,] {
{ 1, 4, 8 },
{ 6, 2, 5 },
{ 9, 7, 3 }
};
matB.Print("matB =");
// 行列(matA)と行列(matA)の積
var matMult = matA.Mult(matB);
matMult.Print("matA matB =");
// 行列(matA)と行列(matA)の加算
var matAdd = matA.Add(matB);
matAdd.Print("matA + matB =");
// 行列(matA)と行列(matA)の減算
var matSub = matA.Sub(matB);
matSub.Print("matA - matB =");
// 行列(matB)の逆行列
var matInverse = matB.Inverse();
matInverse.Print("(matB)-1 =");
// 行列(matA)の転置
var matTranspose = matA.Transpose();
matTranspose.Print("(matA)T =");
// 回転行列の取得
var matRotate = Mat.RotateMat(10.0);
matRotate.Print("RotateMat =");
// 拡大行列の取得
var matScale = Mat.ScaleMat(2.0, 5.0);
matScale.Print("ScaleMat =");
// 平行移動行列の取得
var matTranslate = Mat.TranslateMat(-5.0, 12.0);
matTranslate.Print("TranslateMat =");
Bitmap bmp;
// 画像ファイルを開く
var imgMat = Mat.Imread("0.bmp", out bmp);
imgMat.Print("Image data =", false);
// 画像の表示
var window = bmp.Imshow("Image");
// 配列(画像データ)をcsvファイルに保存
imgMat.SaveCsv("matData.csv");実行画面
サンプルはコンソールプログラムで作成しましたが、Formアプリケーションでも使用可能です。
メソッド
| Add<T>(T[,], T[,]) | 行列の加算を行います。 |
| AddS<T>(T[,], T) | 行列の各要素にスカラー値を加算します。 |
| ArrayToMat<T>(T[]) | 一次元配列からN行1列の行列(二次元配列)に変換します。 |
| Cast<T1, T2>(T1[,]) | 行列の型を変更します。 |
| CloneMat<T>(T[,]) | 行列の型を変更します。 |
| Cross<T>(T[,], T[,]) | 2つのベクトル(3行1列の配列)の外積を計算します。 |
| Degrees(double) | 角度のラジアンから度へ変更します。 |
| Flatten<T>(T[,]) | 行列をN行1列へ変換します。 |
| Hadam<T>(T[,], T[,]) | 行列の各要素の積(アダマール積)を計算します。 |
| Identity<T>(int) | サイズを指定して単位行列を取得します。 |
| Imread(string) | 画像データを行列(Byte型二次元配列)に格納します。 |
| Imread(string, System.Drawing.Bitmap) | 画像データを行列(Byte型二次元配列)に格納し、Bitmapクラスオブジェクトを取得します。 |
| ImreadPlane(string) | 画像データをプレーン(各色ごとの行列)分離し、行列(Byte型二次元配列)に格納します。 |
| ImreadPlane(string, System.Drawing.Bitmap) | 画像データをプレーン(各色ごとの行列)分離し、行列(Byte型二次元配列)に格納し、Bitmapクラスオブジェクトを取得します。 |
| Imshow(System.Drawing.Bitmap, ImagingSolution.Mat.NamedWindow) | Bitmapクラスオブジェクトと表示先ウィンドウを指定して画像を表示します。 |
| Imshow(System.Drawing.Bitmap, string) | Bitmapクラスオブジェクトと表示先ウィンドウタイトルを指定して画像を表示します。 |
| Inverse(double[,]) | 逆行列を求めます。 |
| Inverse(float[,]) | 逆行列を求めます。 |
| Mult<T>(T[,], T[,]) | 行列の積を求めます。 |
| PointToMat(System.Drawing.Point) | Point構造体の座標を3行1列の行列に格納します。 |
| PointToMat(System.Drawing.Point[]) | Point構造体配列の座標を3行N列の行列に格納します。 |
| PointToMat(System.Drawing.PointF) | Point構造体の座標を3行1列の行列に格納します。 |
| PointToMat(System.Drawing.PointF[]) | Point構造体配列の座標を3行N列の行列に格納します。 |
| Print<T>(T[,], bool) | コンソール画面、もしく出力ウィンドウに行列を値を表示します。 |
| Print<T>(T[,], string, bool) | コンソール画面、もしく出力ウィンドウに行列を値を表示します。 |
| PseudoInverse(double[,]) | 擬似逆行列を求めます。 |
| PseudoInverse(float[,]) | 擬似逆行列を求めます。 |
| Radians(double) | 角度の度数(°)からラジアンへ変更 |
| Reshape<T>(T[,], int, int) | 行列のサイズ(行数、列数)を変更します。 |
| RotateAtMat(double, double, double) | 回転角度、回転の中心座標を指定して回転行列(二次元)を取得します。 |
| RotateAtMat(float, float, float) | 回転角度、回転の中心座標を指定して回転行列(二次元)を取得します。 |
| RotateMat(double) | 回転角度を指定して回転行列(二次元)を取得します。 |
| RotateMat(float) | 回転角度を指定して回転行列(二次元)を取得します。 |
| RotateXMat(double) | 回転角度を指定してX軸周りの回転行列(三次元)を取得します。 |
| RotateXMat(float) | 回転角度を指定してX軸周りの回転行列(三次元)を取得します。 |
| RotateYMat(double) | 回転角度を指定してY軸周りの回転行列(三次元)を取得します。 |
| RotateYMat(float) | 回転角度を指定してY軸周りの回転行列(三次元)を取得します。 |
| RotateZMat(double) | 回転角度を指定してZ軸周りの回転行列(三次元)を取得します。 |
| RotateZMat(float) | 回転角度を指定してZ軸周りの回転行列(三次元)を取得します。 |
| SaveCsv<T>(T[,], string) | 行列の値をCSVファイルに保存します。 |
| ScaleAtMat(double, double, double, double) | 拡大率、拡大の基点の座標を指定して拡大行列(二次元)を取得します。 |
| ScaleAtMat(float, float, float, float) | 拡大率、拡大の基点の座標を指定して拡大行列(二次元)を取得します。 |
| ScaleMat(double, double) | 拡大率を指定して拡大行列(二次元)を取得します。 |
| ScaleMat(double, double, double) | 拡大率を指定して拡大行列(二次元)を取得します。 |
| ScaleMat(float, float) | 拡大率を指定して拡大行列(二次元)を取得します。 |
| ScaleMat(float, float, float) | 拡大率を指定して拡大行列(三次元)を取得します。 |
| Sub<T>(T[,], T[,]) | 行列の減算を行います。 |
| SubS<T>(T[,], T) | 行列の各要素からスカラー値を減算します。 |
| SwapRows<T>(T[,], int, int) | 行列の行の値を入れ替えます。 |
| TranslateMat(double, double) | 移動量を指定して、平行移動行列(二次元)を取得します。 |
| TranslateMat(double, double, double) | 移動量を指定して、平行移動行列(三次元)を取得します。 |
| TranslateMat(float, float) | 移動量を指定して、平行移動行列(二次元)を取得します。 |
| TranslateMat(float, float, float) | 移動量を指定して、平行移動行列(三次元)を取得します。 |
| Transpose<T>(T[,]) | 行列の転置行列を求めます。 |
| NamedWindow.Imshow(System.Drawing.Bitmap) | Bitmapクラスオブジェクトを指定し画像表示用ウィンドウに画像を表示します。 |
| NamedWindow.NamedWindow(string) | ウィンドウタイトルを指定し画像表示用ウィンドウを作成します。 |
行列の設定
行列には.NET Framework標準の二次元配列を用います。
行列の値を設定は、以下のように行います。
// 行列(matA)の設定例
var matA = new double[3, 3];
matA[0, 0] = 1; matA[0, 1] = 2; matA[0, 2] = 3;
matA[1, 0] = 4; matA[1, 1] = 5; matA[1, 2] = 6;
matA[2, 0] = 7; matA[2, 1] = 8; matA[2, 2] = 9;
// 行列(matB)の設定例
var matB = new double[,] {
{ 1, 4, 8 },
{ 6, 2, 5 },
{ 9, 7, 3 }
};行列の値の表示
行列(二次元配列)の値はPrint()メソッドを用いるとコンソール画面(フォームアプリの場合は出力ウィンドウ)に配列の型とサイズの行の次に配列の値が表示されます。
コード例
var matA = new double[,] {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 }
};
matA.Print();出力例(コンソールアプリの場合)
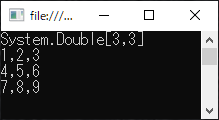
出力例(フォームアプリの場合)
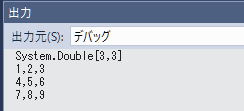
Print()メソッドの引数に文字列を渡すと、先頭行に文字列が表示されます。
matA.Print("matA =");出力例
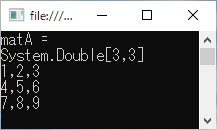
行列の行数が10行より大きい場合は、途中の行が省略されて表示されます。
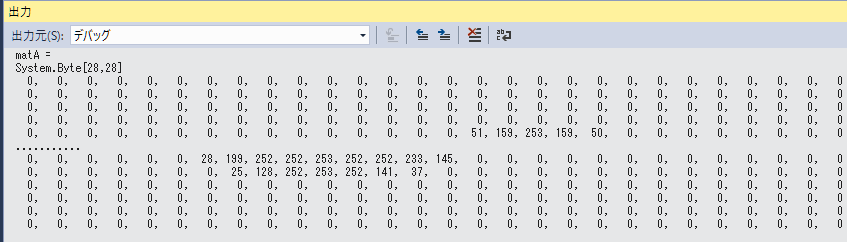
省略しない場合は、引き数にfalseを追加します。
コード例
// 先頭行付き表示
matA.Print("matA =", false);
// 先頭行なしの場合
matA.Print(false);出力例
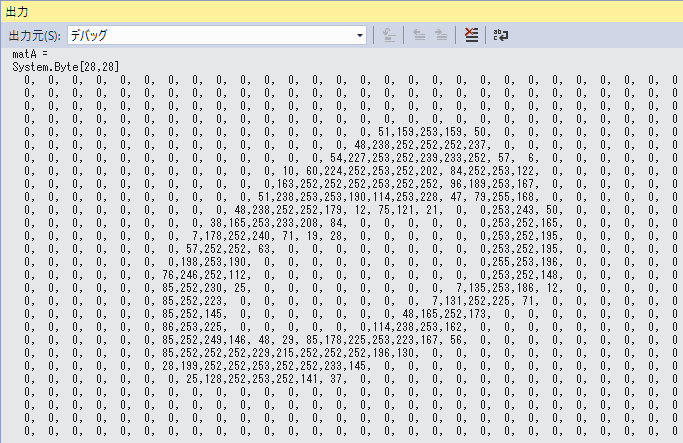
行列の演算
行列演算のメソッドは拡張メソッド形式で形式で作成しています。
好みに合わせてお使い下さい。
コード例
var matA = new double[,] {
{ 1, 2, 3 },
{ 4, 5, 6 },
{ 7, 8, 9 }
};
var matB = new double[,] {
{ 1, 4, 8 },
{ 6, 2, 5 },
{ 9, 7, 3 }
};
// 行列の積(従来の書き方)
var mat1 = Mat.Mult(matA, matB);
// 行列の積(拡張メソッドの書き方)
var mat2 = matA.Mult(matB);
// 逆行列(従来の書き方)
var mat3 = Mat.Inverse(matB);
// 逆行列(拡張メソッドの書き方)
var mat4 = matB.Inverse();行列の演算では、行列のサイズ(行数、列数)が不正だったり、逆行列が解けない場合、メソッド内で例外が発生します。
例外は嫌な場合は、事前にサイズチェックや、try~catchによるエラー処理を行って下さい。
画像の読込、表示、CSVファイル保存
画像の読込、表示、CSVファイル保存を行うには、以下のコードで行います。
コード例
Bitmap bmp;
//画像ファイルを開く
var matImg = Mat.Imread("0.bmp", out bmp);
// 画像データの表示
matImg.Print(false);
// 画像の表示
bmp.Imshow("画像");
// CSVファイル保存
matImg.SaveCsv("image.csv");画像ファイルをImread()メソッドで開くと、Byte型の二次元配列(Byte[,])に輝度値が格納されます。
カラー画像の場合、B,G,R,B,G,R…の順で輝度値が格納されます。
Imread()メソッドとは別に、ImreadPlane()メソッドで画像ファイルを開くと、各プレーン(色)ごとに二次元配列の配列(Byte[][,])に輝度値が格納されます。プレーンの順番はB,G,Rの順となります。
実行結果
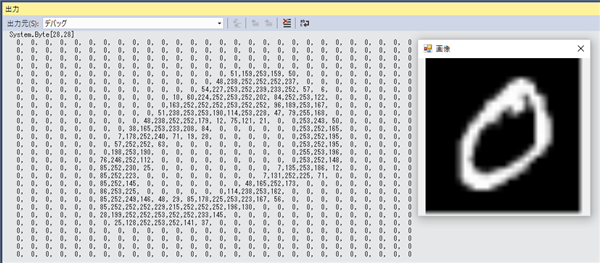
画像の表示のメソッド Imshow()は、メソッドが呼ばれるたびに新しいウィンドウが作成されます。
コード例
// 画像の表示
bmp.Imshow("画像");
bmp.Imshow("画像");
bmp.Imshow("画像");実行結果
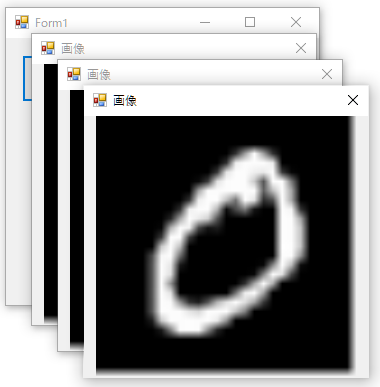
毎回、ウィンドウを生成しないようにするには、あらかじめNamedWindowsクラスを生成し、Inshowメソッドへ渡してください。
コード例
// ウィンドウの生成
var win = new Mat.NamedWindow("画像");
// 画像の表示
bmp.Imshow(win);
bmp.Imshow(win);
bmp.Imshow(win);画像の表示機能は、基本的にデバッグ機能です。
より多くの機能を追加したい場合は、FormやPictureBoxを用いて画像を表示してください。
その他
ライブラリファイル(ImagingSolution.Mat.dll)と同じフォルダにXMLファイル(ImagingSolution.Mat.xml)を配置すると、メソッドのヒントが表示されるので、そちらも合わせて参照してください。

擬似逆行列を用いた二次式近似の例
擬似逆行列を用いた例はこちらのページ
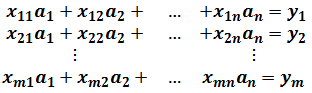
でExcelを用いて二次式の近似式を解いていますが、これと同じ計算を、この行列演算ライブラリを用いて計算してみたいと思います。
二次式近似は、ざっくり言うと、二次式を
![]()
としたとき、式を変形し、
![]()
とします。
このとき、xとyのデータを用いて以下のような行列を作成し、
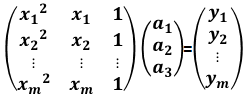
行列部分を記号で表すと、
![]()
となるところを、擬似逆行列を用いて、Aの行列を解けば、二次式の未知数を解くことができます。
![]()
この処理を行列演算ライブラリを使い、C#プログラムにすると、
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using ImagingSolution;
namespace ConsoleApplication1
{
class Program
{
static void Main(string[] args)
{
// 近似データ
var dataX = new double[] { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 };
var dataY = new double[] { 10, 9, 6, 12, 15, 21, 34, 36, 48, 52 };
var mat = new double[dataX.Length, 3];
for (int i = 0; i < dataX.Length; i++)
{
mat[i, 0] = dataX[i] * dataX[i];
mat[i, 1] = dataX[i];
mat[i, 2] = 1;
}
mat.Print();
// 配列から行列(N行1列)へ変換
var matY = dataY.ArrayToMat();
matY.Print();
// 擬似逆行列で二次式の係数を解く
var ans = mat.PseudoInverse().Mult(matY);
// 解の表示
ans.Print();
// 近似式を表示
Console.WriteLine($"y = {ans[0,0]}x^2 + {ans[1, 0]}x + {ans[2, 0]}");
// キー入力待ち
Console.WriteLine("続行するには何かキーを押してください . . .");
Console.ReadKey();
}
}
}となり、実行結果は
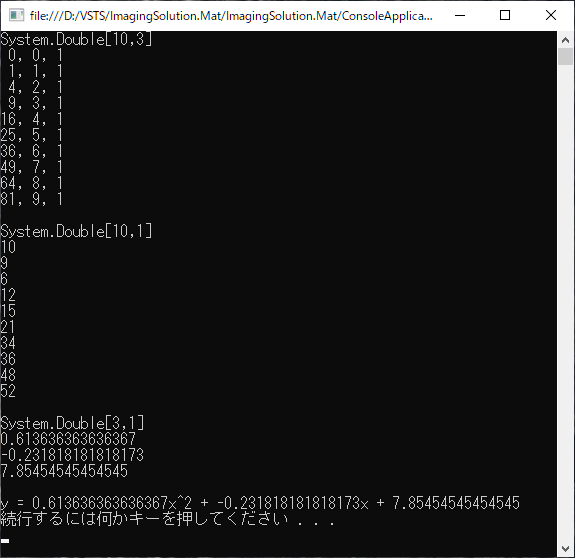
となります。
最後の計算式の表示は微妙ですが、Excelの結果と比べてみても
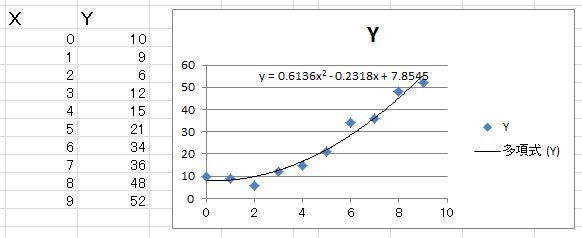
見事、C#の結果とExcelの結果が一致することができました!!

コメント