「Python アフィン変換」と検索すると、OpenCVを使った説明が多いような気がしますが、画像を表示するだけなら、Pillowにtransform()メソッドというのがあり、これもなかなか高機能な処理が可能になります。
Pillowならtkinterとの相性もいいので、GUIで画像をウィンドウに表示したいのなら、おススメです。
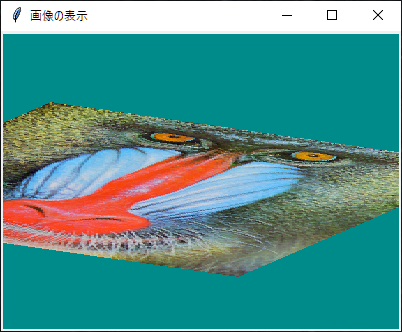
最終的には、以下のようにウィンドウに画像を表示するのが目標です。
transformメソッドの構文
Image.transform(size, method, data=None, resample=0, fill=1, fillcolor=None)| パラメータ | 説明 |
| size | (幅, 高さ)のタプル |
| method | 変換方法
|
| data | methodにより内容が異なります。
|
| resample | 画素補間方法
|
| fill | ??? |
| fillcolor | 出力先の画像の外側の背景色 |
(参考)
https://pillow.readthedocs.io/en/stable/reference/Image.html#PIL.Image.Image.transform
アフィン変換のサンプルプログラム
画像ファイルを読み込み、30°回転 → 横2倍、縦0.5倍 → 横+50、縦+70の平行移動 を行うサンプルを示します。
import numpy as np # アフィン変換行列演算用
import tkinter as tk
from PIL import Image, ImageTk # 画像データ用
class Application(tk.Frame):
def __init__(self, master = None):
super().__init__(master)
self.pack()
self.master.title("画像の表示") # ウィンドウタイトル
self.master.geometry("400x300") # ウィンドウサイズ(幅x高さ)
# Canvasの作成
back_color = "#008B8B" # 背景色
canvas = tk.Canvas(self.master, bg = back_color)
# Canvasを配置
canvas.pack(expand = True, fill = tk.BOTH)
# アフィン変換行列(numpy ndarray)
# 30°回転→横2倍、縦0.5倍→横+50、縦+70の平行移動の例
# 回転行列(30°回転)
rad = np.radians(30) # 30°をラジアン単位へ変換
r = np.array([
[np.cos(rad), -np.sin(rad), 0],
[np.sin(rad), np.cos(rad), 0],
[0, 0, 1]
])
# 拡大縮小(横2倍、縦0.5倍)
s = np.array([
[2, 0, 0],
[0, 0.5, 0],
[0, 0, 1]
])
# 平行移動(横+50、縦+70)
t = np.array([
[1, 0, 50],
[0, 1, 70],
[0, 0, 1]
])
# アフィン変換行列の計算(回転→拡大縮小→平行移動の順)
affine = np.matmul(t, np.matmul(s, r))
# 等倍のとき、単位行列
#affine = np.identity(3)
# アフィン変換を使った画像の表示
self.disp_image(canvas, "./Mandrill.bmp", affine, fillcolor = back_color)
def disp_image(self, canvas, filename, affine, method = Image.AFFINE, resample = Image.NEAREST, fillcolor = None):
'''画像をCanvasに表示する
canvas :表示先のCanvasオブジェクト
filename :表示する画像ファイルパス
affine :画像データ→表示先へのアフィン変換行列
method :アフィン変換(Image.AFFINE)、射影変換(Image.PERSPECTIVE)
resample :補間方法:ニアレストネイバー(Image.NEAREST)、バイリニア(Image.BILINEAR)、バイキュービック(Image.BICUBIC)
fillcolor :画像の外側の色
'''
# キャンバスのサイズを取得(Canvasのサイズに合わせています)
self.master.update()
size = (canvas.winfo_width(), canvas.winfo_height())
# PIL.Imageで開く
pil_image = Image.open(filename)
# アフィン変換行列の逆行列の計算
affine_inv = np.linalg.inv(affine)
# アフィン変換行列を一次元のタプルへ変換
affine_tuple = tuple(affine_inv.flatten())
# アフィン変換で画像を変換
pil_image = pil_image.transform(
size, # 出力サイズ(幅, 高さ)
method, # 変換方法
affine_tuple, # アフィン変換行列(出力→入力への変換行列)
resample, # 補間方法
1,
fillcolor # 画像の外側の背景色
)
#PIL.ImageからPhotoImageへ変換する
self.photo_image = ImageTk.PhotoImage(image=pil_image)
# 画像の描画
canvas.create_image(
0, 0, # 画像表示位置
anchor = tk.NW, # 画像表示位置の基準(左上)
image=self.photo_image # 表示画像データ
)
if __name__ == "__main__":
root = tk.Tk()
app = Application(master = root)
app.mainloop()(実行結果)

アフィン変換(method = PIL.Image.AFFINE)で使う時のポイント
transform()メソッドの第3引数(data)に渡す引数にアフィン変換行列のデータを渡すのですが、transform()メソッドのアフィン変換行列は出力先から元画像へ変換するアフィン変換行列となります。
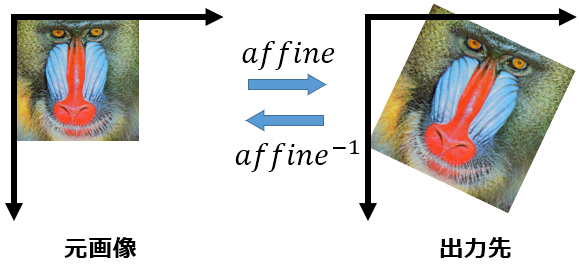
ただし、一般的には元画像から出力先へのアフィン変換で考える場合が多いので、元画像から出力先へのアフィン変換行列(affine)を計算して、最後にアフィン変換行列の逆行列(affine-1)をtransform()メソッドの data へ渡します。
つまり、変換前の座標を(x, y)、変換後の座標を(x’, y’)とすると、アフィン変換の行列は
$$\left(\begin{array}{c}x^{‘}\\ y^{‘}\\ 1\end{array}\right)=
\left(\begin{array}{c}a & b & c\\ d & e & f \\ 0 & 0 & 1\end{array}\right)
\left(\begin{array}{c}x\\ y \\ 1\end{array}\right)$$
となりますが、この逆の変換を計算し、
$$\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)=
\left(\begin{array}{c}a & b & c\\ d & e & f \\ 0 & 0 & 1\end{array}\right)^{-1}
\left(\begin{array}{c}x^{‘}\\ y^{‘} \\ 1\end{array}\right)$$
から、逆行列の部分を
$$\left(\begin{array}{c}a^{‘} & b^{‘} & c^{‘}\\ d^{‘} & e^{‘} & f^{‘} \\ 0 & 0 & 1\end{array}\right)=
\left(\begin{array}{c}a & b & c\\ d & e & f \\ 0 & 0 & 1\end{array}\right)^{-1}$$
と置くと、transform()メソッドの第3引数(data)へは
$$data = (a^{‘}, b^{‘}, c^{‘}, d^{‘}, e^{‘}, f^{‘})$$
となるタプルを渡せばOKです。(サンプルプログラムではタプルの要素数を9個指定してますが、使わない部分を渡しても大丈夫なようです。)
アフィン変換の行列の計算部分については、行列の積、逆行列が計算できるnumpyを使うと便利だと思います。
(参考)
https://imagingsolution.net/program/python/numpy/matrix_operation/
また、アフィン変換の座標系ですが、画像の左上原点(左上の画素のさらに左上が原点)で、右方向が+X方向、下方向が+Y方向、時計回りが+θ方向となります。
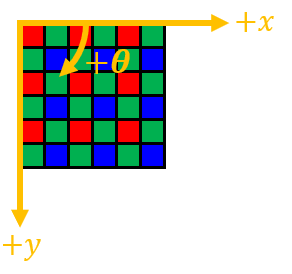
ちなみに、C#では左上の画素の中心が原点(0, 0)でした。
(参考)
https://imagingsolution.net/program/csharp/image_coordinate/
参考ページ
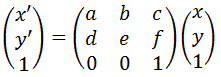
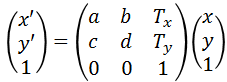






コメント
他のページも含めて解りやすい説明が多く、非常に役立ちました!
感謝です。
コメントありがとうございます!
ブログのモチベーションにつながります。