【C#】正規分布に従う乱数の取得

.NETでは乱数のクラスにRamdomクラスがあります、どれも一様に分布する乱数しか取得できません。

例えば、NextDoubleメソッドを用いると、0以上、1.0未満の一様に分布した乱数を取得する事ができます。

var rnd = new Random(); 

for (int i = 0; i < 1000; i++) 
{ 
	Console.WriteLine(rnd.NextDouble().ToString()); 
}

上記プログラムで出力した値をExcelでヒストグラムにしてみると、０～１．０の一様？？な乱数が取得させていることが分かります。

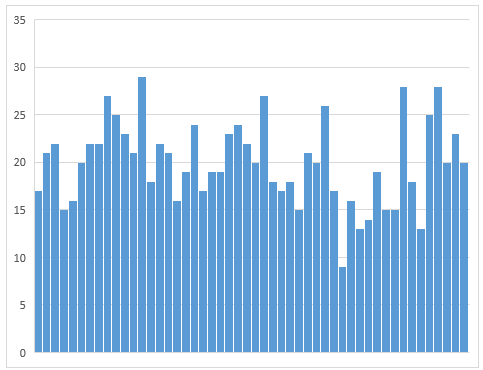
正規分布に従う乱数を取得するには、今回はボックス＝ミュラー法という手法で乱数をしてみます。

XとYがお互いに独立で、0～１の範囲で一様に分布する乱数のとき

$${ Z }_{ 1 }=\sqrt { -2\log { X } } cos(2\pi Y)\\ { Z }_{ 2 }=\sqrt { -2\log { X } } sin(2\pi Y)$$

のZ₁、Z₂はそれぞれ標準偏差１．０、平均値０．０の正規分布に従う乱数となります。

（参考）ボックス＝ミュラー法 Wikipedia

ボックス＝ミュラー法 - Wikipedia

ja.m.wikipedia.org

これをC#のプログラムにしてみると

var rnd = new Random(); 

double X, Y; 
double Z1, Z2; 

for (int i = 0; i < 1000; i++) 
{ 
	X = rnd.NextDouble(); 
	Y = rnd.NextDouble(); 
	
	Z1 = Math.Sqrt(-2.0 * Math.Log(X)) * Math.Cos(2.0 * Math.PI * Y); 
	Z2 = Math.Sqrt(-2.0 * Math.Log(X)) * Math.Sin(2.0 * Math.PI * Y); 

	Console.WriteLine(Z1.ToString()); 
	Console.WriteLine(Z2.ToString()); 
}

という感じ。

コンソールに吐き出された値をExcelでヒストグラムにしてみると

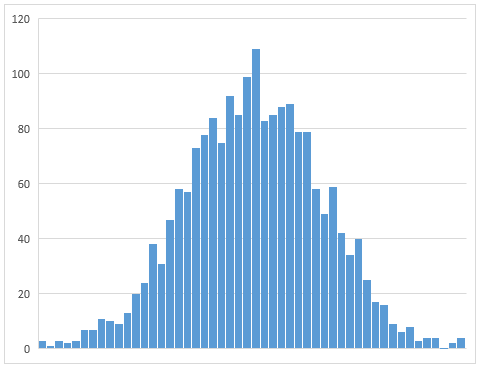
となり、確かに正規分布に従った感じの分布となりました。
標準偏差１．０、平均値０．０ではなく、標準偏差sigma、平均値ave　のときの乱数が欲しい場合は

Z1 = sigma * Math.Sqrt(-2.0 * Math.Log(X)) * Math.Cos(2.0 * Math.PI * Y) + ave;
Z2 = sigma * Math.Sqrt(-2.0 * Math.Log(X)) * Math.Sin(2.0 * Math.PI * Y) + ave;

となります。

←　C#へ戻る