ガウス(Gauss)の消去法は連立一次方程式を解くのに用いられます。
基本的な方針は、下記のような連立一次方程式
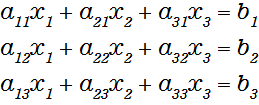
を行列であらわすと、
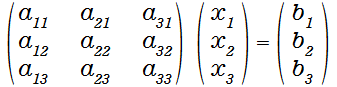
となりますが、対角成分を全て1、左下の成分を0になるように、行の入替えや足し算、引き算などを行い、下記の行列になるように調整します。
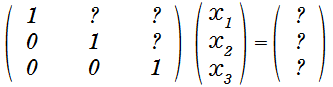
(?の部分は任意の値で可)
これまでの処理を前進消去といいます。
ここで、最後の行の部分(X3の部分)に着目すると、答えが確定しています。
この値を使って最後から2行目の値を計算すると答えが算出できます。
このように最後の行から順々に計算すると答えが全て計算することができます。
この処理は後退代入といいます。
この前進消去と後退代入の処理を合わせてガウスの消去法といいます。
さらに、前進消去のときに対角成分を1にするときの割り算の計算のときにおいて、
ピボット選択を行ったGauss-Jordan法でも説明しましたが、
- 0(ゼロ)で割ることはできない。
- 値を絶対値の小さい値で割ると、値に誤差が含まれる場合、計算結果に大きく影響が出てしまう。
という性質を考慮します。
ということで、以下、具体的な計算例を示します。
連立一次方程式
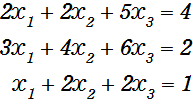
のうち、まず最初にX1の項のどれか1つを1にするのですが、割り算の計算で誤差が少なくなるように、X1の係数が一番大きい2行目の式を一番上に持ってきます。
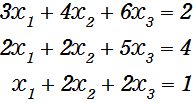
次に1行目の式のX1の係数が1になるように1行目の式全体をX1の係数(3)で割ります。
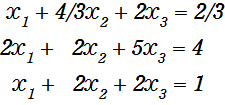
次に1行目以下の式のX1の項が消えるように、
2行目-1行目×2 、 3行目-1行目を計算します。
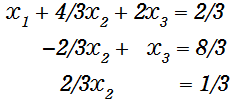
ここで、3行目の式のX3の項(行列で表現すると対角成分)が消えてしまったので、
このままだと対角成分を1にできないので、2行目と3行目を入れ替えます。
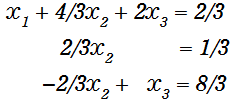
次に2行目の式のX2の係数を1にするように、2行目の式全体に3/2を掛けます。
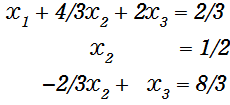
次に2行目以下のX2の項が消えるように3行目+2行目 × 2/3を計算します。
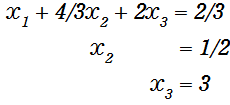
3行目の式のX3の係数はすでに1なので、前進消去はこれで終了です。
この3本の式を行列であらわすと
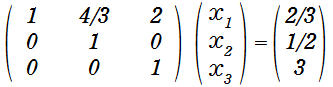
というように、対角成分が全てが1で左下の成分が0になったことが分かります。
次に後退代入です。
一番下の行の式はすでに答えが確定(X3 = 3)しているのがわかります。
一番下の答えを用いて、下から2行目の式の答えを計算、
一番下、下から2行目の答えを用いて下から3行目の式の答えを計算していきます。
(今回の例だけ特別に、下から2行目の式の答えが確定してしまっています。)
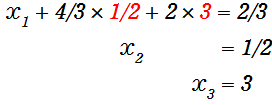
こうして全ての答えが求まります。
![]()
この一連の処理がガウスの消去法です。
このガウスの消去法を用いると、連立方程式を求めたり、最小二乗法の未知数を
求めることができます。



コメント
[…] 5/19 ガウスの消去法 […]