外積を用いて三角形の面積を求める方法を紹介します。
まず、外積のおさらいですが、三次元ベクトルにおいて2つのベクトルの外積の大きさが2つのベクトルからなる平行四辺形の大きさに一致する特徴がありました。
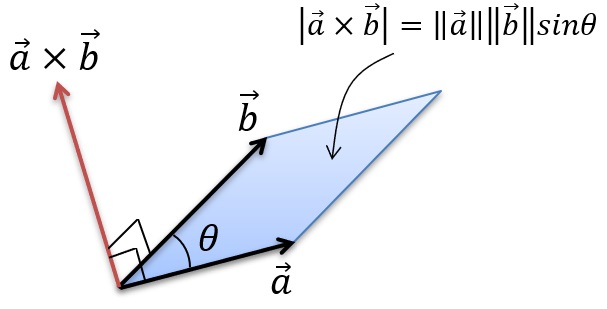
この2つのベクトルのZ成分を0(ゼロ)にして二次元座標へ応用します。
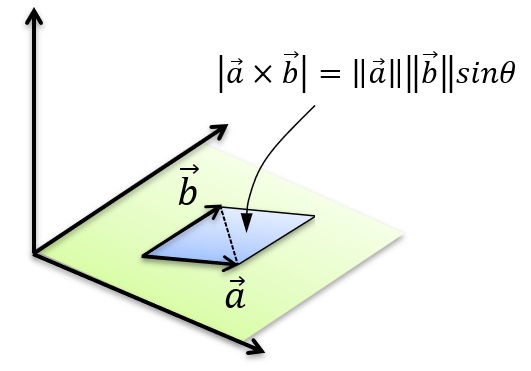
2つのベクトルを
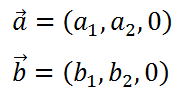
とすると、2つのベクトルの外積は、x成分とy成分は0(ゼロ)となり、z成分の大きさが平行四辺形の面積の大きさとなる事から、3点からなる三角形の面積は平行四辺形の半分の大きさとなり、
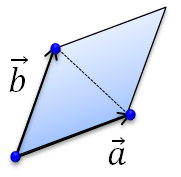
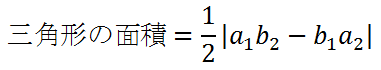
となります。
例題
3点、A(1, 3), B(3, 4), A(2, 6)からなる三角形の面積を求めよ。
解)
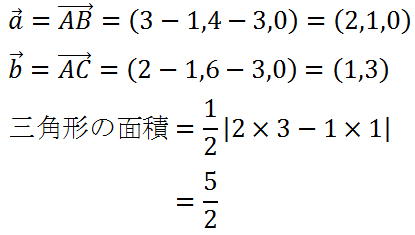

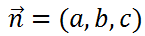
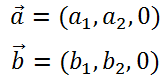
コメント
ありがとうございます。
ここでは3角形と多角形を扱ておりますが、
4角形の場合をお示しいただきたいと思います。
よろしくお願いいたします。
コメントありがとうございます。
四角形の場合(4点の図形)としては書いていないのですが、n角形(n点からなる多角形)の面積としてこちら↓に記載してありますので、そちらを参照ください。
https://imagingsolution.net/math/calc_n_point_area/
説明はとてもよくわかります。でも、b2は何処に行ったのかな?
ご指摘ありがとうございました。
早速、記事も修正しました。
助かりました。
[…] 2/17 3点からなる三角形の面積を求める […]