奇関数
![]()
となる関数。
つまり、関数のグラフが原点に対して対象となります。
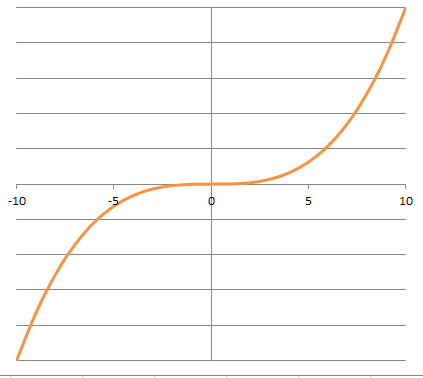
【例】
y = x, y = x3, y = sinθ など
【特徴】
-a ~ a の範囲で積分すると
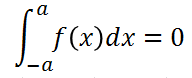
となります。
偶関数
![]()
となる関数。
つまり関数のグラフがY軸に対して対象となります。
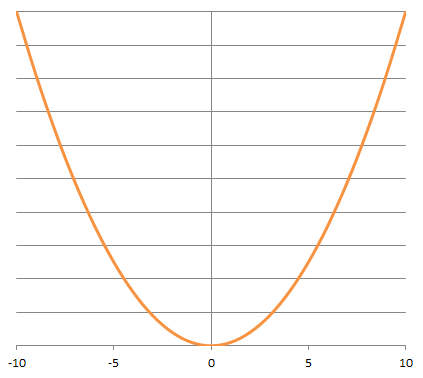
【例】
y = x2, y = x4, y = cosθ など
【特徴】
-a ~ a の範囲で積分すると
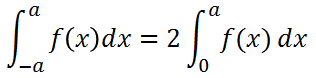
となります。
計算例
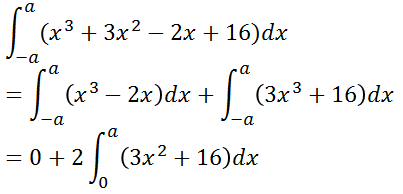
となります。
このように、関数を奇関数と偶関数に分けて積分します。
この偶関数・奇関数の特徴を応用すると、関数の合計値をfor文などで計算する場合に、計算量を大きく減らす事ができるので、処理の高速化が期待できます。

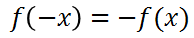

コメント
[…] 奇関数・偶関数でも説明したように、 […]
[…] 4/29 奇関数、偶関数 […]