正規直交基底

正規直交基底はあまり馴染が無いように思いますが、フーリエ変換や主成分分析の理解をするには必要となってきます。

 

【定義】

ベクトルの大きさが１となり、互いのベクトル（任意の２つのベクトル）が 直交するベクトルの組合せ

 

となります。

 

ここで、ベクトルの大きさ（ノルム）が１という事は、そのベクトルは単位ベクトルであり、
ベクトルが直交するということは、ベクトルの内積が０となる事を意味しています。

 

もっとも簡単な例として、二次元ベクトルの場合

 

 

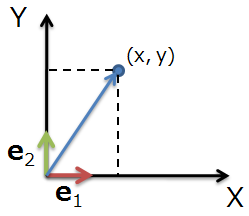
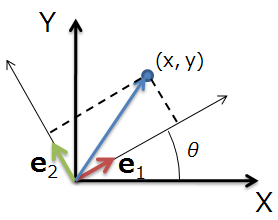
上図のように、e₁, e₂を

 

 

としたとき、この e₁, e₂ は正規直交基底である事は分かると思います。

 

ここで大事なのが、任意ベクトルＶの e₁ 方向の大きさをａ, e₂ 方向の大きさをｂとすると、

 

各ベクトルの方向の大きさは内積で求まる！

 

という特徴があります。

 

上記の例では

 

e₁方向の大きさａは

 

ａ = Ｖ ・ e₁ = X  × 1 + Y × 0= X

 

e₂方向の大きさ ｂ は

 

ｂ = Ｖ ・ e₂ = X  × 0 + Y × 1= Y　

 

となります。この処理を斜影と言います。

 

逆に

 

任意ベクトルは正規直交基底と各大きさを用いて表す事ができる！

 

という特徴もあります。

 

任意ベクトルを求めるには正規直交基底の各ベクトルとその大きさをかけて、ベクトルを足し合わせると求まります。

 

上記の例では

 

　　任意ベクトルＶ 　= ａ  × e₁ + ｂ × e₂
　　　　　　　　　　 = ａ × (1, 0)+ ｂ × (0, 1)
　　　　　　　　　　 =  (ａ, ｂ)

となりますが、この例はあまりにも単純な例なので、もう少しだけ具体的にして、ベクトルを

 

Ｖ 　= （4, 6)

 

正規直交基底を

 

 

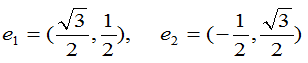
とします。

 

 

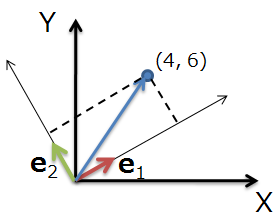
このとき e₁, e₂ が正規直交基底であるかどうか？は、それぞれのベクトルの大きさと、内積を計算すると確認する事が出来ます。

 

 

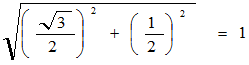
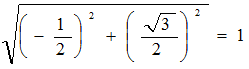
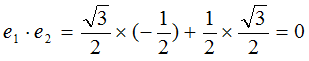
また、このとき、

 

e₁方向の大きさａは

ａ = Ｖ ・e1 =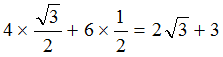

 

e₂方向の大きさｂは

ｂ = Ｖ ・e2 =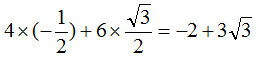

 

となります。
逆にベクトルＶを正規直交基底の e₁,e₂ とそれぞれの向きの大きさを用いて計算すると

 

 

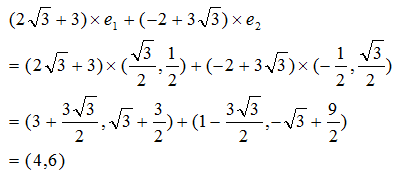
となり、確かに正規直交基底を用いると任意ベクトルを表すことができそうです。

 

このことをもう少し一般化して、正規直交基底 e₁,e₂ を

 

 

としても、任意ベクトルＶ　を表すことはできます。

 

 

これをさらに三次元の場合でも、任意ベクトルＶ　を表すことができます。

 

 

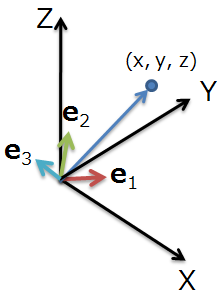
このノリでさらにｎ次元の場合でも同様に正規直交基底をe₁,e₂・・・,e_ｎとしても、任意ｎ次元ベクトルＶ　を表すことができます。

ということで、クドいですが、正規直交基底には

 

任意ベクトルを正規直交基底と各大きさを用いて表す事ができる！

 

という特徴があります。

 

それって、もうほとんどフーリエ変換の説明になっているのですが、お気づきでしょうか？
フーリエ変換についてはいづれ記事にしたいと思います。