下図のように点(x0, y0, z0)を通り、法線ベクトルが
![]()
の平面の方程式は
a(x-x0)+b(y-y0)+c(z-z0)=0
となり、一般に
ax+by+cz+d=0
と表します。
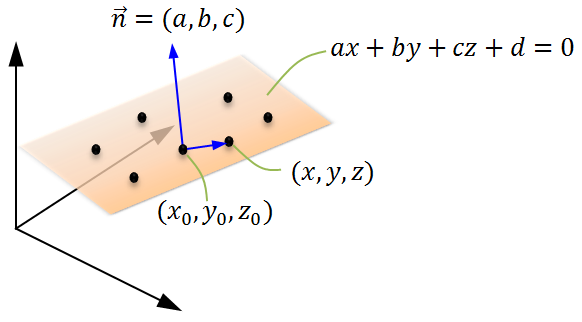
なぜそうなるのか?というと、平面に垂直な法線ベクトルと、平面上の任意の2点からなるベクトルとは常に垂直である事から、法線ベクトルと、平面上の2点からなるベクトルとの内積の結果は常に0となります。
つまり、法線ベクトル(a, b, c)と平面上の2点のベクトル(x-x0, y-y0, z-z0)の内積が0となるので、
a(x-x0)+b(y-y0)+c(z-z0)=0
となり、これを展開したのが、平面の方程式
ax+by+cz+d=0
となります。
平面は点が3つあれば求まるのですが、3点から平面の式を求めるには外積を用います。
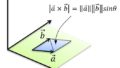
外積では2つのベクトルの外積を求めると、2つのベクトルと外積の結果とは直交するという特徴があるので、下図のように
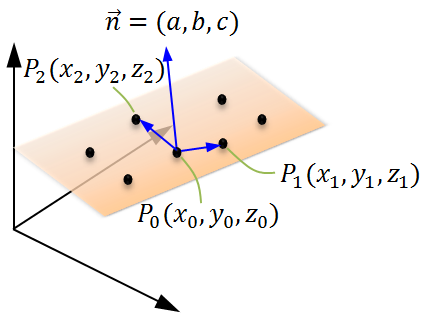
平面上の3点P0, P1, P2から、P0→P1、P0→P2の2つのベクトルを作り、
(x1-x0, y1-y0, z1-z0)
と
(x2-x0, y2-y0, z2-z0)
の外積を計算すると、法線ベクトルの各成分(a, b, c)は
a=(y1-y0)×(z2-z0)-(y2-y0)×(z1-z0)
b=(z1-z0)×(x2-x0)-(z2-z0)×(x1-x0)
c=(x1-x0)×(y2-y0)-(x2-x0)×(y1-y0)
となり、法線ベクトルの要素のa, b, cが求まるので、平面の方程式に3点P0, P1, P2のどれかを代入すると平面の方程式が求まります。

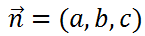
コメント