二次元座標(X,Y座標)の場合のアフィン変換行列についてはこちらで説明しましたが、今回は三次元座標(X,Y,Z座標)のアフィン変換となります。
三次元座標の場合、まず座標軸の定義、回転方向の定義を明確に覚えます。
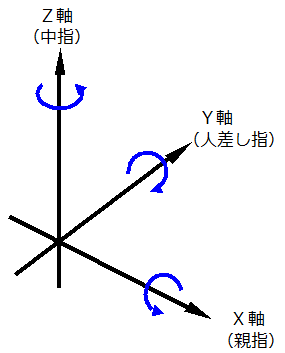
この座標は右手座標系と呼ばれます。
フレミングの法則のときのように右手で親指、人差し指、中指をそれぞれ
直交するようにします。
このとき親指から順に親指がX軸、人差し指がY軸、中指がZ軸の方向と
なります。
回転方向は電流と磁界の向きと同じように電流が軸の向き、磁界が回転方向
に相当します。(右ねじの法則と同じです。)
回転行列
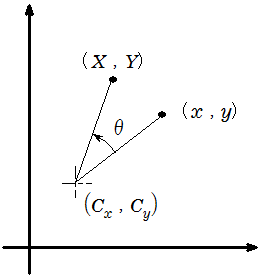
三次元の回転行列の前に二次元の回転行列のおさらいです。
二次元の回転行列は以下の通りとなります。
これをベースに三次元座標の場合では、回転する軸の正の方向から原点の方向を見たときに、X軸、Y軸はそれぞれ何軸に相当するのか?を考えれば、二次元座標のXやYの変数の置き換えで導き出すことができます。
行列変換しない軸に関しては単位行列でそのまま残します。
【X軸周りの回転】
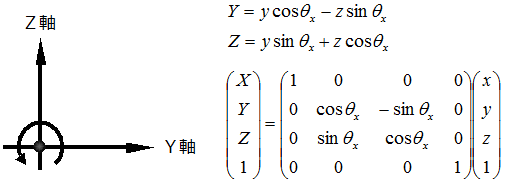
【Y軸周りの回転】
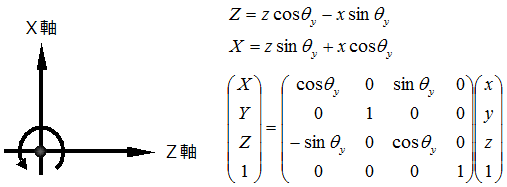
【Z軸周りの回転】
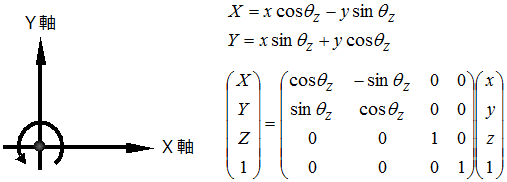
拡大縮小行列
点(x, y, z)を原点に関してX軸方向にSX倍、Y軸方向にSY倍、Z軸方向にSZ倍する行列は
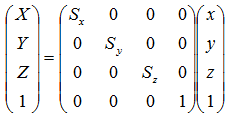
平行移動行列
点(x, y, z)をX軸方向にTX、Y軸方向にTY、Z軸方向にTZだけ移動する行列は
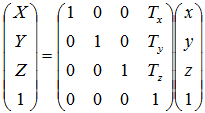
補足
三次元の座標変換に関して検索すると座標変換は下記のように
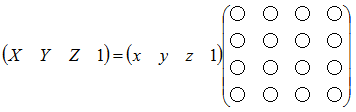
行ベクトルで表記される場合もあるのですが、変換行列の値が変わるので、
混同しないようご注意下さい。
この表現はマイクロソフトがお得意で、DirectX(Direct3D)や.NETのアフィン変換でしか使われないので、特に必要の無い場合は覚えない方が無難です。
関連記事
二次元座標のアフィン変換についてはこちら↓にまとめています。
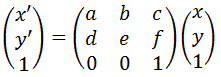

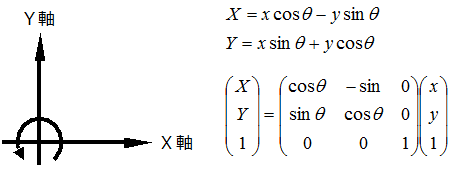
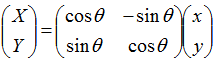
コメント
リンクしました。ありがとうございました。
https://ja.stackoverflow.com/questions/76305/pythonで-三角すいの体積の計算を座標からしました
ちょっと面白そうだったので、自分なりに解いてみましたが、中学校入試の問題でなければ、三角形PQRの面積をベクトルPQとベクトルQRの外積で求めて、外積から三角形の面に対する単位法線ベクトルを求めて、法線ベクトルとベクトルPSとの内積で三角形PQRの面からSまでの高さが出るので、あとは、三角形の面積と高さで三角錐の面積を求めちゃいますね。
という発想は、たぶん、三次元グラフィックスをやっている人なら、やりそうなパターンですね。
ご回答ありがとうございます。
例えば、四角形の立方体を画面中心に置き、3次元の移動や回転したりしたいのです。
軸を固定するのではなく軸も回転させたいです。
説明が分かり辛く申し訳ありません。
色々と試してみます。
動画やunityのリンクありがとうございます!
参考にさせていただきます。
お世話になっております。
いつも楽しく勉強させてもらっています。
現在c#で3D描画を勉強しています。
3次元のxyz軸それぞれの回転計算式は分かるのですが、
ではその計算結果をどのようにしてPictureBoxなどのx,yの
2次元座標空間に落とし込めばいいのかが理解できないでいます。
お手数なのですが、x,y,z飲みは3つの座標をx,yに変換する方法を
ご教示いただけないでしょうか?
以上、よろしくお願いいたします。
yukiさん、コメントありがとうございます。
3Dで、どんな物をどのように表示するか?でやり方が変わってくるのですが、
●三次元座標の点を表示したいだけなら
ここの記事で紹介している三次元座標のアフィン変換にさらに追加して、表示用のアフィン変換を掛けた結果の座標(x,y,z)の(x,y)だけを描画すれば、Z軸方向から見た座標をPictureBoxに表示できると思います。
●ポリゴン(三角形の面のあつまり)で立体を表示したいなら
私のブログでは紹介していませんが、Direct3DやOpenGLを使う事になると思います。
やり方は、コメント欄でお教え出来るほど単純では無いため、別のブログや書籍を参考にしてみてください。
ちなみに、仕事でやった内容ですが、OpenGLを使って、C#のプログラムに表示した例の動画です↓
https://youtu.be/L3kzdWcsAp0
●その他
私はやった事がありませんが、Unityを使って3D表示ができるかも?しれません。
https://docs.unity3d.com/ja/2018.4/Manual/vuforia_get_started_displaying_3d_content.html
ご参考まで。