回転行列、拡大縮小行列、平行移動行列

本記事は、私がアフィン変換を勉強し始めた当初の記事になります。
今では、3×3行列の同次座標行列と呼ばれる行列しか用いておらず、こちらの方が断然おススメなので、下記ページを参照ください。

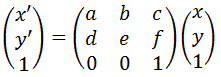
アフィン変換（平行移動、拡大縮小、回転、スキュー行列）

画像の拡大縮小、回転、平行移動などを行列を使って座標を変換する事をアフィン変換と呼びます。 X,Y座標の二次元データをアフィン変換するには、変換前の座標を（x, y）、変換後の座標を（x',y'）とすると回転や拡大縮小用の２行２列の行列と、...

imagingsolution.net

2011.03.24

以下は、2×2行列を使ったアフィン変換の説明です。

回転行列

点（x, y）を原点まわりに反時計方向にθ度回転する行列は

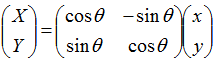
拡大縮小行列

点（x, y）を原点に関してＸ軸方向にＳ_Ｘ倍、Ｙ軸方向にＳ_Ｙ倍する行列は

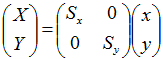
平行移動行列

点（x, y）をＸ軸方向にＴ_Ｘ、Ｙ軸方向にＴ_Ｙだけ移動する行列は

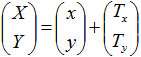
ただし、平行移動だけ行列の足し算になると、扱いにくい場合があるので３×３行列を用いて以下のように表す場合もあります。
というより、こちらを使う方が便利です。（私はこちらしか使いません。）

【回転行列】

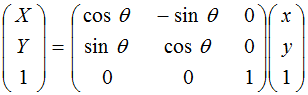
【拡大縮小行列】

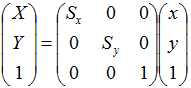
【平行移動行列】

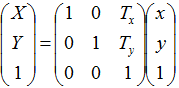
とすることで、すべての座標変換を行列の積で扱うことができます。

この行列を同次座標行列と言います。
詳細はこちらを参照ください。

参考まで．．．

個人的には回転行列を覚えるのは苦手で、ＳｉｎとＣｏｓが逆になっりマイナスのつける位置を間違ったりしていたのですが、次のように考えることで少しは覚えやすくなりました。

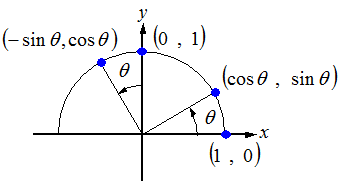
下図のように

点（１，０）をθ度回転すると（Ｃｏｓθ、Ｓｉｎθ）
点（０，１）をθ度回転すると（－Ｓｉｎθ、Ｃｏｓθ）

に移動することはすぐにわかります。

このことを行列で表現すると
点（１，０）が（Ｃｏｓθ、Ｓｉｎθ）になることから

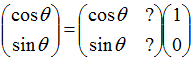
点（０，１）が（－Ｓｉｎθ、Ｃｏｓθ）になることから

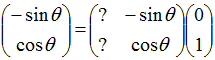
という事がわかります。
これを合わせて表現すると

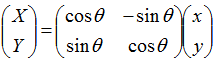
となり、回転行列が求まります。
この計算を何回か繰り返すと、そのうち覚えると思います。

←使える数学へ戻る