行列で連立方程式を解く

行列を使って連立方程式を解く方法を紹介します。

【計算例】

３つの方程式

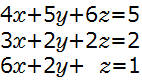
を行列であらわすと

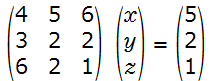
となります。この行列を逆行列を使ってＸ、Ｙ、Ｚに関して解くと

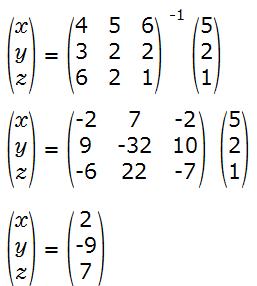
となり連立方程式を行列で解くことができます。

…というのは普通すぎて面白くないので、３点からなる円の方程式を行列で解く方法を紹介します。

中心（a、b）、半径　ｒ　の円の方程式

(X – a)² + (Y – b)² = r²

を展開して

X² + Y² – 2aX – 2bY + a² + b² – r² = 0

となり、A = 2a、B = 2b、C = r² – a² – b² とおくと、上式は

AX + BY + C = X² + Y²

となります。

ここで、円上の３点（X₀、Y₀）、（X₁、Y₁）、（X₂、Y₂）を代入すると

AX₀ + BY₀ + C = X₀² + Ｙ₀²
AX₁ + BY₁ + C = X₁² + Ｙ₁²
AX₂ + BY₂ + C = X₂² + Ｙ₂²

の３本の式が成り立ち、これを行列で表現すると、

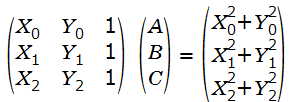
となり、Ａ、Ｂ、Ｃに関して行列を解くと

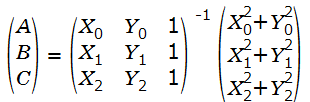
となり、A、Ｂ、Ｃが求まることから、A = 2a、B = 2b、C = r² – a² – b² より
中心と半径を求めることができます。

行列を解く部分は

のページを参照下さい。