回転行列では原点周りに点を回転させますが、任意の点(Cx、Cy)周りに回転させたい場合にはどうするのか?
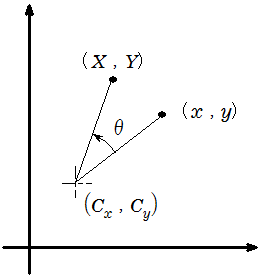
これまでの知識を少し応用することで、意外と簡単に求めることができます。
まず、回転する点を回転中心座標が原点と一致するように点を移動させます。
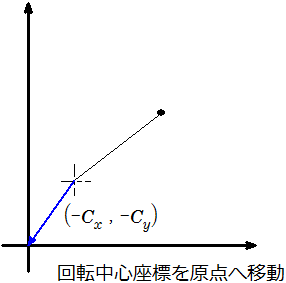
次に移動した点を原点周りに回転移動させます。
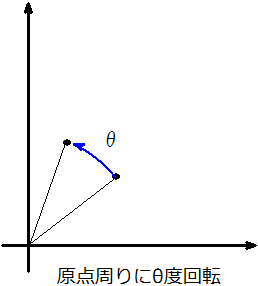
回転移動後、点を原点から元の回転中心位置へ移動させます。
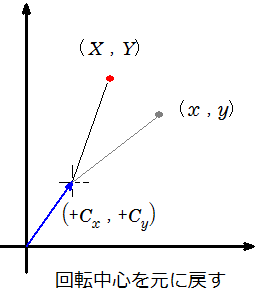
これで、任意点(Cx、Cy)周りに点を回転移動させることができました。
この 原点へ移動→原点周りの回転→元へ戻す の一連の処理を行列であらわすと

行列部分を整理すると
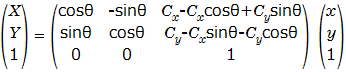
となり、任意点(Cx、Cy)周りに点を回転移動させる行列を求めることができます。
今回は回転移動について説明しましたが、拡大縮小についても、任意点を基点に拡大縮小する場合についても同様です。
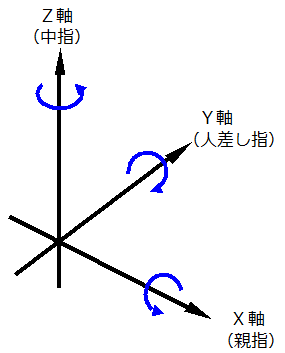
この考え方は、二次元の座標だけでなく、三次元の場合も使えます。。
参考
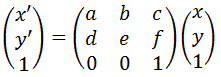
アフィン変換(平行移動、拡大縮小、回転、スキュー行列)
画像の拡大縮小、回転、平行移動などを行列を使って座標を変換する事をアフィン変換と呼びます。X,Y座標の二次元データをアフィン変換するには、変換前の座標を(x, y)、変換後の座標を(x',y')とすると回転や拡大縮小用の2行2列の行列と、平...

コメント