 お知らせ
お知らせ フリーの数値演算ライブラリ
私のお世話になっている会社が無償で数値演算ライブラリを公開してくれました。数値演算ライブラリ eyemLib内容的には行列演算(ベクトル演算)、近似計算、幾何計算、計算幾何、キャリパー(寸法計測)向け処理、二次元点群マッチング、カメラキャリ...
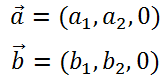 使える数学
使える数学 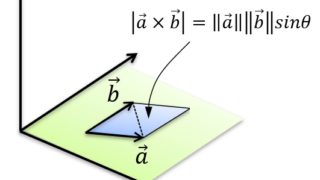 使える数学
使える数学 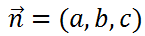 使える数学
使える数学 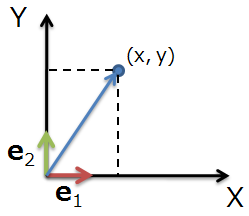 使える数学
使える数学 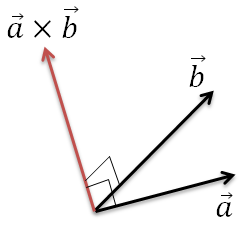 使える数学
使える数学 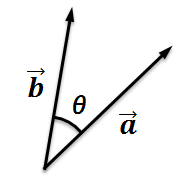 使える数学
使える数学 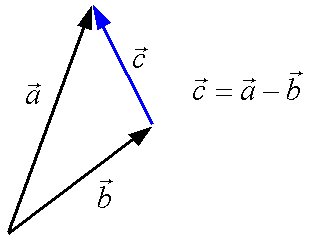 使える数学
使える数学 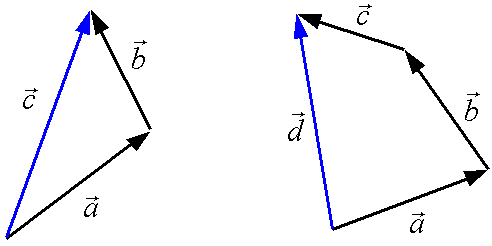 使える数学
使える数学 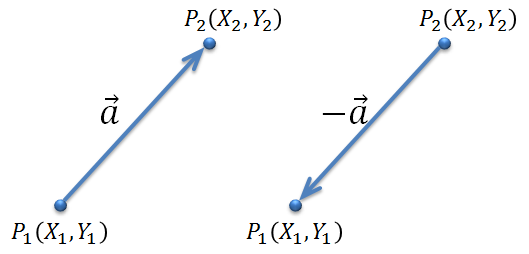 使える数学
使える数学 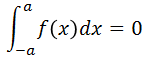 使える数学
使える数学 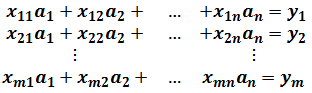 使える数学
使える数学 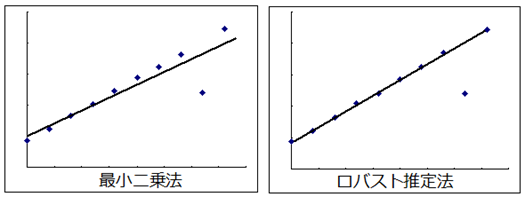 使える数学
使える数学  使える数学
使える数学