外積

外積は内積ほどは応用する事は出来ないのですが、外積を用いる事で、平面の向きの計算（ポリゴンの法線ベクトルの計算）や、２つのベクトルのなす平行四辺形の面積の計算、２つのベクトルのなす角度の計算などに応用できます。
２つのベクトルのなす角度については、内積でも計算できますが、外積を使うと、２つのベクトルの位置関係により、角度の値の＋、－を使い分けることが可能になります。

 

内積の定義は以下の通りです。

 

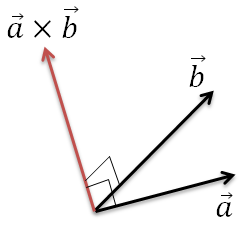
三次元空間における２つのベクトル

 

 

において、ベクトルa とベクトルb の外積は、以下のようになります。

 

 

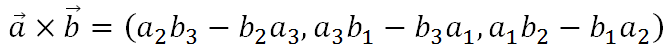
この外積の計算は少し覚えづらいのですが、ベクトルa とベクトルbの成分を上下に並べて、Ｘ成分を求める時はＸ成分を隠して、残りの４つの成分で下図のように斜めに掛けて引く、いわゆるたすき掛けという計算を行います。（と言っておきながら、私は覚えてないので、毎回調べてます．．．）

 

 

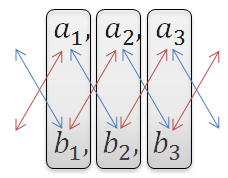
また、内積の計算結果はただの値（スカラー）でしたが、外積の結果はベクトルとなります。

 

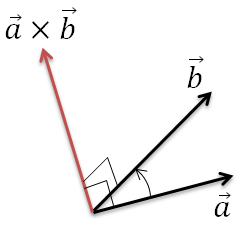
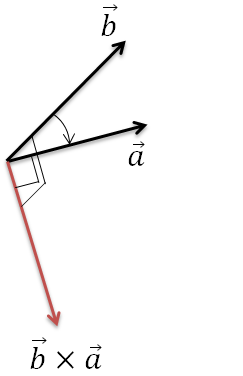
ベクトルなので、外積の結果は向きと大きさを持ち、外積の向きは右ねじの方向となります。

（右ねじの回転方向は外積の掛ける順番となります。）

 

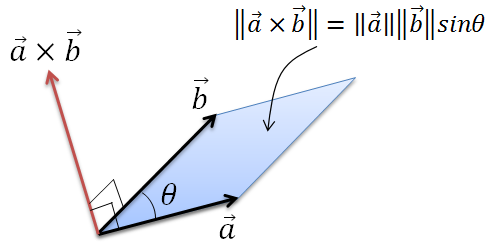
さらに外積の大きさ（ノルム）は２つのベクトルでなす平行四辺形の面積と一致します。

 

 

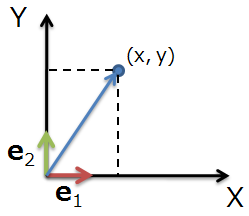
また、２つのベクトルが三次元の場合と言いましたが、二次元のベクトルであってもベクトルのＺ成分を０（ゼロ）にする事で外積の特徴を応用する事も可能です。

 

←使える数学へ戻る