逆行列(Gauss-Jordan法)

２×２行列の逆行列

行列

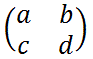
の逆行列は

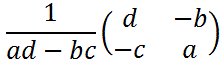
となります。
ただし、ad-bc = 0 のとき、逆行列は存在しません。

逆行列を解く手法はいくつかありますが、ここでは比較的分かり易いGauss-Jordan法を紹介します。

Gauss-Jordan法では行列の右側に単位行列を付けたして、行ごとに掛け算、足し算、引き算を行い、行列の左側が単位行列になるように計算を繰り返し、最後に右側に残った行列が逆行列となります。

といっても分かりづらいと思うので、具体的な計算例は以下の通りです。

行列

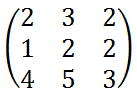
の右側に単位行列を追加します。

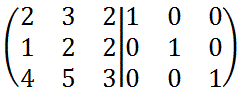
１行１列目の要素が１となるように１行目を２で割ります。

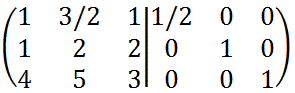
１列目の要素が（１　０　０）となるように

[２行目] = [２行目]ー[１行目]
[３行目] = [３行目]ー[１行目]×４

を計算します。

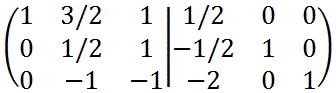
２行２列目の要素が１となるように２行目を２倍します。

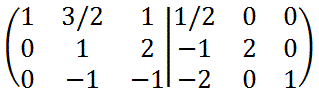
２列目の要素が（０　1　０）となるように

[１行目] = [１行目]ー[２行目]×３/２
[３行目] = [３行目]＋[２行目]

を計算します。

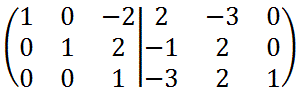
ここで、３行３列目の要素はすでに１なので、３列目の要素が（０　０　１）となるように

[１行目] = [１行目]＋[３行目]×２
[２行目] = [２行目]ー[３行目]×２

を計算します。

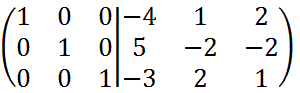
これで、左側が単位行列となり、右側に出来た行列が求める逆行列となります。

ただ、このままの方法では、求める行列の対角要素（行数と列数の同じ場所）に０（ゼロ）がある場合は対角要素を１に出来ない（０で割れない）ので、ここにピボット選択という手法を導入します。
このピボット選択についてはピボット選択を行ったGauss-Jordan法にて紹介しています。