拡大、縮小
XとYであらわせる関数
![]()
をX軸方向に Sx 、Y軸方向に Sy 倍の拡大縮小すると
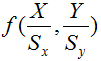
となります。
(拡大の場合、Sx,Syは1以上、縮小の場合、Sx,Syは1以下となります。)
回転移動
関数 f(X,Y)を原点周りにθ度回転すると
![]()
となります。
平行移動
関数 f(X,Y)をX軸方向に Tx 、Y軸方向に Ty だけ平行移動すると
![]()
となります。
拡大縮小してから平行移動した場合は
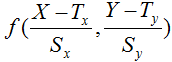
となります。
考え方
グラフ(関数)を拡大、縮小、回転、平行移動するときに、実際にX、Yの値の変換は全て逆!つまり
| 拡大の場合 | 縮小 |
| θ度回転の場合 | -θ度回転 |
| +方向へ移動の場合 | -方向へ移動 |
の処理をしています。
何だかとっても違和感がありますが、グラフ(関数)を移動していると思うのではなく、グラフ(関数)はそのままに、XY軸を変換していると思うと、少しはしっくり来るでしょうか...
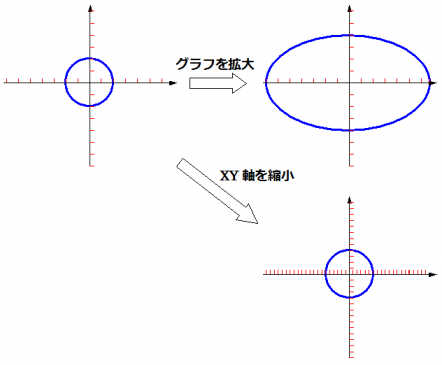
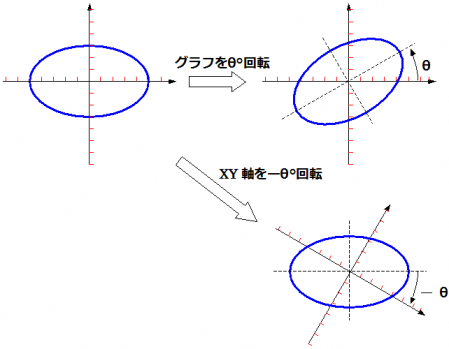
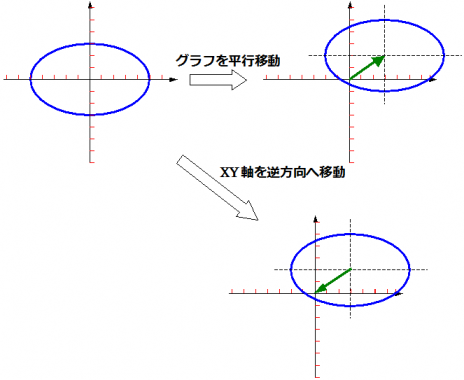
また、拡大縮小、回転、平行移動を同時に行う場合は、変換の順番に注意が必要です。
行列の計算と同じように、計算の順番が異なると計算結果も異なります。基本的には
拡大縮小 ⇒ 回転 ⇒ 平行移動
の順番で変換を行うのが、一番よいでしょう。
もちろん、分かっていて別の順番で変換するのは構いません。
具体例
半径1の円の式、グラフは
![]()
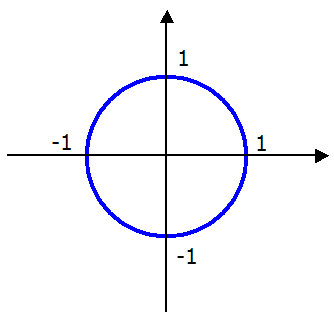
となり、このグラフをX軸方向に Sx 、Y軸方向に Sy 倍の拡大縮小すると
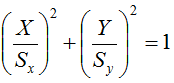
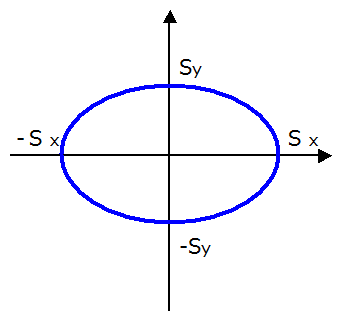
となります。
式を変形すると楕円の公式そのものとなります。
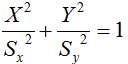
さらにX軸方向に Tx 、Y軸方向に Ty だけ平行移動すると
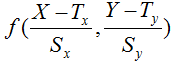
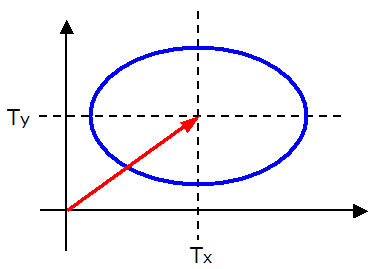
となり、円のグラフを拡大縮小、平行移動することで楕円の一般式となります。
応用例
2点を通る直線の式を、グラフの平行移動の考え方を用いて求めます。
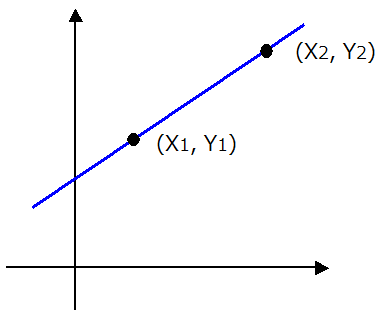
2点を通る直線の式は
![]()
より、よくある直線の式の解き方は、XとYに2点の座標を代入して、2つの式を作成し、連立方程式を用いて、未知数の a と b を求めると思います。
しかし、直線の傾き a はグラフを見て分かる通り、(Yの増分)/(Xの増分)であるから
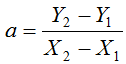
となり、あとは切片の b を求めるだけになります。
ここで、少し見方を変えて、原点を通る傾き a のグラフを下図のように
原点(0,0)から点(X1、Y1)へ平行移動します。
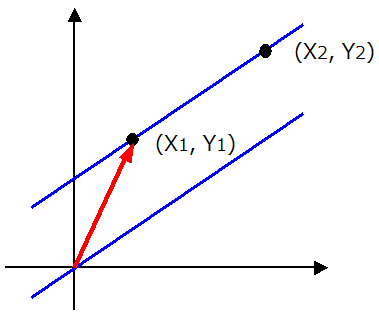
これを式であらわすと
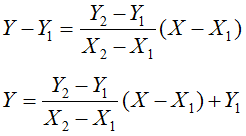
となり、直線の式を求めることができます。
この式をそのまま覚えている方もいると思いますが、グラフの拡大縮小、平行移動の
考え方は汎用的に使うことができ、応用範囲がとても広がります。
他にも
Y = sinθ
という波形に関して、
Y軸方向の拡大率は振幅
θ軸方向の拡大率は周期
θ軸方向の平行移動は位相のズレ
というように、置き換えて考えることもできます。
このように考えるようになると、高校時代に一生懸命覚えたけど、すぐに忘れてしまうこのへんの公式↓
| sin ( – θ ) = – sin θ | cos ( – θ ) = cos θ |
| sin ( 90°+ θ ) = cos θ | sin ( 90°- θ ) = cos θ |
| cos( 90°+ θ ) = – sin θ | cos ( 90°- θ ) = sin θ |
| sin ( 180°+ θ ) = – sin θ | sin ( 180°- θ ) = sin θ |
| cos ( 180°+ θ ) = – cos θ | cos ( 180°- θ ) = – cos θ |
は全て拡大縮小、平行移動として考えることが出来ます。
例えば sin ( 90°- θ ) は sin ( -(θ – 90°) ) と書きかえると
sin波形をθ方向に-1倍(Y軸に対して対称移動)してから、+θ方向に90°平行移動すれば良い事が分かります。
最初に手元にsin波形を描いておけば、変換後、どのような波形になるのか?は見ればわかりますよね?!

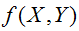
コメント