内挿と外挿

内挿（Interpolation）と外挿(Extrapolation)という言葉は、最近ではDeep Learning関連で目にする事が多い気がしますが、内挿・外挿とは、データを近似し、データ以外の場所を推定する際に、データの範囲内を推定することを内挿といい、データの範囲外を推定することを外挿といいます。

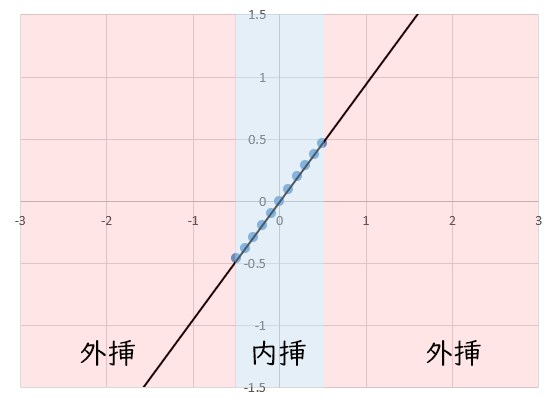
しかしながら、一般的に外挿で推定した値は必ずしも正しいとは限らないため、しない方が良いといわれます。以下に推定した値が正しくならない例を示します。

外挿した値が近似したモデル（近似式）とはズレる場合

下図の例は、かなり恣意的ではありますが、データを近似し、データの範囲内で他のデータを推定する内挿の場合では誤差は少ないですが、データの範囲外を推定する外挿ではデータの変化の傾向が異なり誤差が大きくなる可能性もあります。

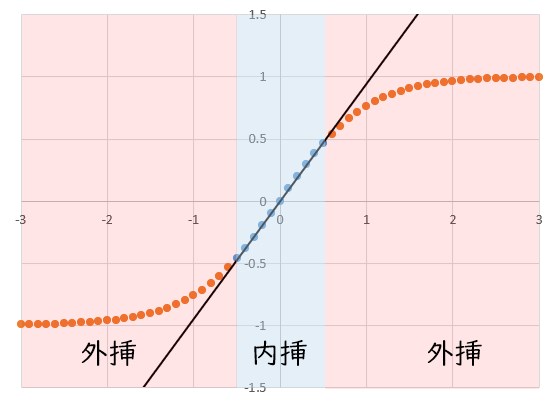
このことはDeep Learningでも言われる事ですが、データを学習する際は、様々な状態のデータを学習させ、推論する際は学習させたデータの範囲内に留めておく必要があります。

外挿となってしまう場合は学習データを追加し、推論するデータがデータの範囲内になるようする必要があります。

外挿は誤差が大きくなりやすい

前項の例は、内挿と外挿のデータの傾向が異なる場合の例として示しましたが、内挿と外挿とでデータの傾向が同じ場合でも外挿の方が誤差が大きくなる場合があります。

例えば、内挿、外挿とも直線的に変化することが分かっている場合に、２点のデータを使って直線で近似する場合もよくあります。

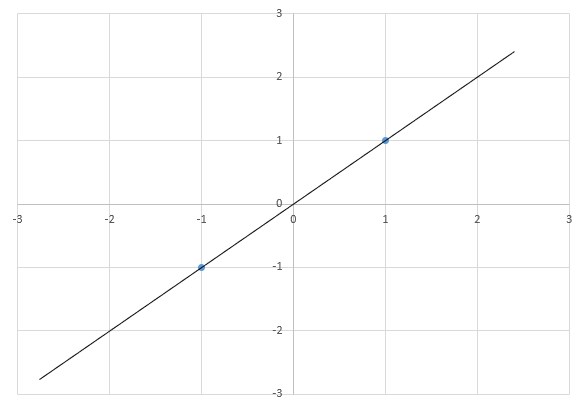
しかしながら、近似に用いたデータにも、少なからず誤差が含まれる場合がほとんどです。

この時に２点のデータから計算した直線も、下図のように誤差が出てしまいます。

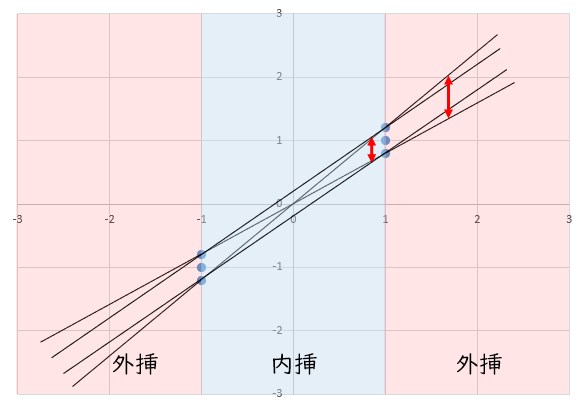
上図を見ても分かるように、近似に持ちるデータに誤差が含まれたとしても、内挿の範囲内であれば、計算した直線もデータの誤差の範囲内に収まりますが、外挿になるとデータの誤差が増幅され、計算した直線は、データの誤差以上の誤差となってしまいます。

以上のことから、内挿はいいけれども、外挿をする場合には注意が必要となります。