合成関数の微分

Deep Learningをお勉強していたら、合成関数の微分が出てきたのですが、もう３０年ぶりぐらいに見たので、その復習です。

\(y=f(u), u=g(x)\)としたとき、\(y=f(g(x))\)を合成関数とよび、この合成関数を\(x\)に関して微分すると、

$$\frac{ dy }{ dx } =\frac { dy }{ du } \frac { du }{ dx } \\ \quad =\frac { d }{ du } f(u)\frac { d }{ dx } g(x)$$

となります。

合成関数を教わったときは、合成関数の微分は「外側の微分ｘ内側の微分」って覚えてたような。。

試しに\(y=sin({ x }^{ 2 })\)の微分は\(u={ x }^{ 2 }\)と置くと

$$\frac { dy }{ dx } =\frac { d }{ du } f(u)\frac { d }{ dx } g(x)\\ \quad =cos(u)\times 2x\\ \quad =cos({ x }^{ 2 })\times 2x$$

これをPythonのmatplotlibを使ってグラフにしてみると

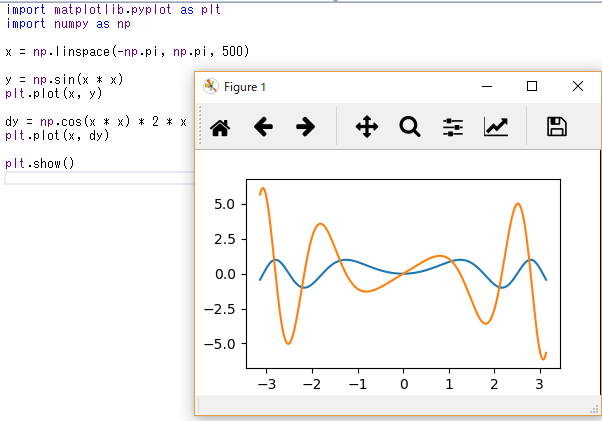
となり、青の線の微分（傾き）がオレンジ色の線なので、合ってそう。