標準偏差の説明としては、
標準偏差はデータのバラツキを表す
というのが多いでしょうか?
その性質からデータの誤差などの指標としても用いられる事が多くあります。
しかしながら、 標準偏差=バラつき とだけ覚えていると、実際に標準偏差を用いる時に、思わぬ落とし穴にハマる場合があります。
そこで、標準偏差の式を改めて眺めてみると
$$\sigma =\sqrt { \frac { 1 }{ n } \sum _{ i=1 }^{ n }{ { \left( { x }_{ i }-\overline { x } \right) }^{ 2 } } } $$
となっています。
この式が何の計算をしているのか?を言葉で表すと
全データの平均(\(\overline { x } \))と各データ(\({ x }_{ i }\))の差の2乗の平均の平方根
を計算しています。
この計算を図示すると下図のようになります。
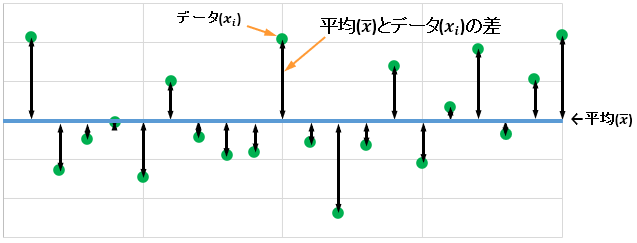
平均とデータの差の二乗の平均をルートした値が標準偏差です。
それでは、具体的に標準偏差を計算するとどうなるのか?を見ていきたいと思います。
問題1)AとBのデータの標準偏差は、どちらが大きいでしょうか?
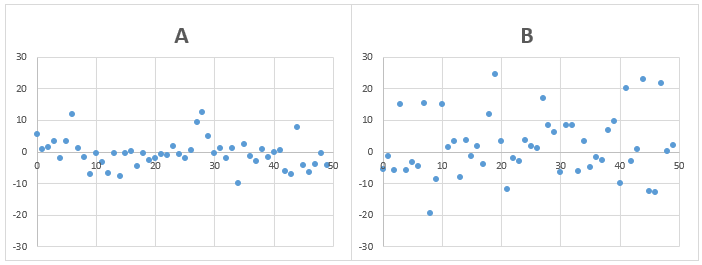
答え)B
平均とデータの差が全体的に大きいBのデータの方が標準偏差が大きくなります。
問題2)AとBのデータの標準偏差は、どちらが大きいでしょうか?
AとBのデータのばらつきは、ほぼ同じでデータの個数が異なる場合
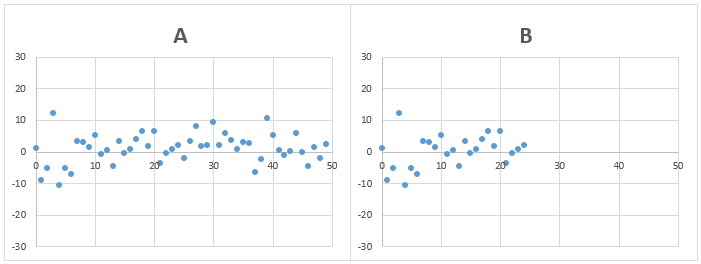
答え)AとBもほぼ同じ
バラつきの具合が同じ場合、データの個数が変化しても、標準偏差は平均とデータの差の二乗の平均のルートを計算しているので、標準偏差の値はほぼ同じになります。
ただし、データ個数の少ないBの方がデータの個数が少ないため、1つ1つのデータに平均の値が影響されやすくなり、標準偏差の値が各データの値に依存しやすく(標準偏差の値がバラつきやすく)なります。
ここまでは、標準偏差=バラつき と思っていても問題にならない場合ですが、次からは注意が必要な場合の例を示します。
問題3)AとBのデータの標準偏差は、どちらが大きいでしょうか?
AとBのデータのばらつきは、ほぼ同じでデータの個数が異なります。
ただし、1点だけ大きく平均からズレたデータが含まれます。
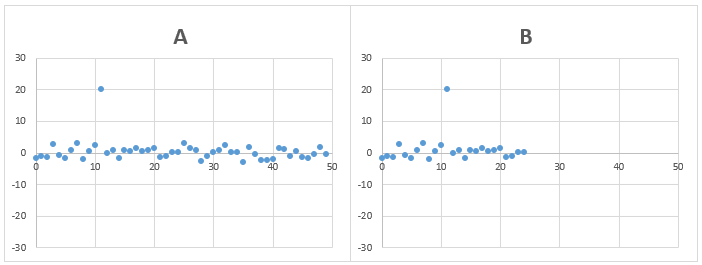
答え)B
AとBのデータのバラつき具合は、一見、同じように見えますが、平均とデータの差の二乗の値の合計をデータ個数で割る際に、データ個数の少ないBの方が値としては大きくなるため、標準偏差はBの方が大きくなります。
問題4)AとBのデータの標準偏差は、どちらが大きいでしょうか?
Aのデータは前半25個のデータと、後半25個のデータは同じ。
BのデータはAのデータの前半25個のみ
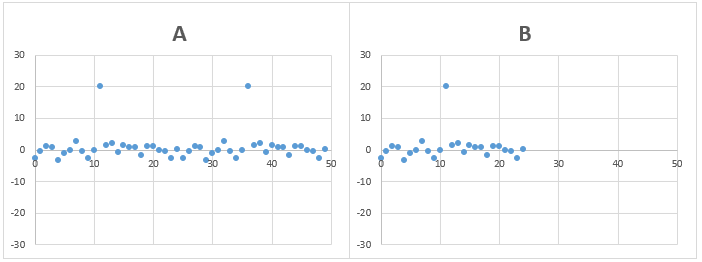
答え)AとBも同じ
一見、Aのデータの方が大きな誤差を含む点が2点(Bのデータは1点)あるため、Aの方が標準偏差の値が大きくなるように見えなくもありませんが、全データの平均と各データの差の2乗の平均の値(分散という)が同じになるため、標準偏差も同じになります。
問題5)AとBのデータの標準偏差は、どちらが大きいでしょうか?
Bのデータは、Aのデータに比べ、細かいデータのバラつきは小さいですが、全体的にデータが傾いています。
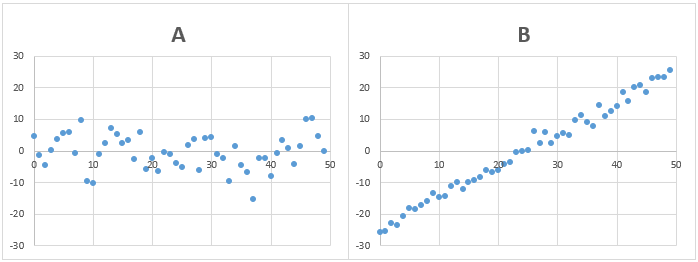
答え)B
全データの平均と各データの差の2乗の平均の値がBの方が大きくなるため、標準偏差もBの方が大きくなります。
問題6)AとBのデータの標準偏差は、どちらが大きいでしょうか?
Bのデータは、Aのデータに比べ、細かいデータのバラつきは小さいですが、全体的にデータが歪んでいます。
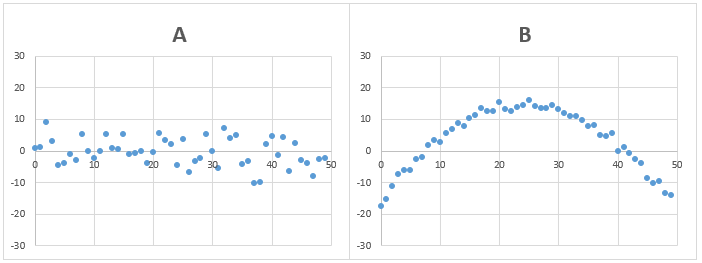
答え)B
問題5と同様に、全データの平均と各データの差の2乗の平均の値がBの方が大きくなるため、標準偏差もBの方が大きくなります。
まとめ
問題1~6に示したように、人の目で見たデータのバラつきの大きさと、標準偏差の値の大小とは、必ずしも一致しない場合があります。
そのため、 標準偏差=バラつき とだけ認識するのではなく、標準偏差の計算である
標準偏差 = 全データの平均と各データの差の2乗の平均の平方根
として、計算方法を言葉で覚えておく事をおススメします。
それでは、人の感じるバラつきと一致するような値を求めるには、どうすれば良いのか?を考えると、決まりきった計算方法は知らないのですが、問題3のようにデータの個数が異なるデータを比較する場合は、標準偏差の計算をデータ全体で計算するのではなく、部分的に標準偏差を計算すると、ある領域ではAとBのバラつきは同じだが、他の領域ではAの方がバラつきが小さい事が分かります。
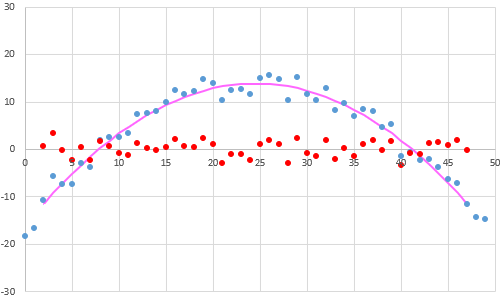
問題5、問題6のようにデータ全体に傾きや歪みがある場合は、ガウシアンフィルタなどのノイズ除去処理を強めにかけて(下図の紫の線)、そのノイズ除去された値と各データの値の差(下図の赤の点)に関して標準偏差を計算すると、データ全体の傾きや歪みに影響される事なく、バラつきを求める事ができます。
←使える数学へ戻る


コメント