簡単には解けない複雑な計算式の解を求める手法の一つに二分法という手法があります。
これは、2点間の間に必ず解がある場合、2点間の半分の位置の値を求め、解が小さい方にあるのか?大きい方にあるのか?を確認し、解がある方のさらに半分の位置の値を求め...と解のある位置を追い込む手法です。
説明が難しいので具体例で示します。
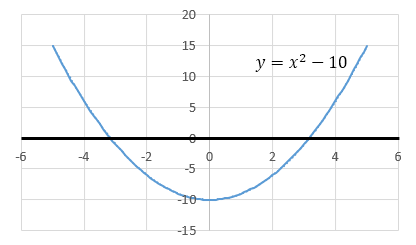
下図は y = x2 – 10 のグラフですが、y=0 となるxの値を求める場合の例です。
この例では、普通に解を求める事ができますが、あえて二分法で解きます。
y=0 となるxの値は、-4 ~ -2 と 2 ~ 4 の間にありそうな事はわかります。
今回は 2 ~ 4 の間にある解を求めます。
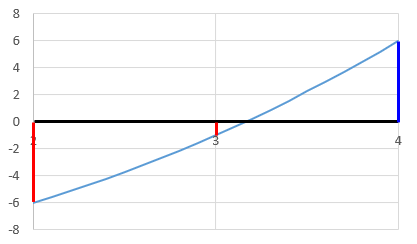
2と4の中間の3の時のyの値を計算すると、yの値は負になるので、y=0となるxの値は
3 ~ 4 の間にあることがわかります。
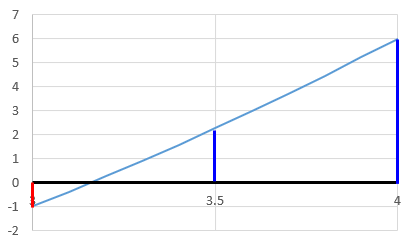
さらに、3と4の中間の3.5の時のyの値を計算すると、yの値は正になるので、
y=0となるxの値は3 ~ 3.5 の間にあることがわかります。
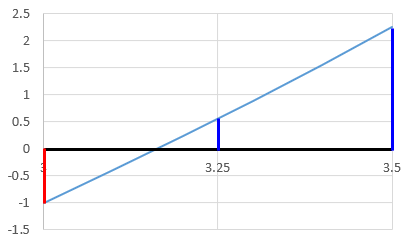
さらに、3と3.5の中間の3.25の時のyの値を計算すると、yの値は正になるので、
y=0となるxの値は3 ~ 3.25 の間にあることがわかります。
・・・と、この処理を2点間の範囲が十分小さくなるまで繰り返すことで、y=0 となる値を求める手法が二分法となります。
二分法の考え方は非常に簡単ですが、個人的には数式の解を求めるために使うことは、ほとんど無く、二分法の考え方を応用することはよくあります。
その一例を示したいと思います。
プログラムのエラーの場所を特定する場合
プログラム中のどこかでエラーが発生しているときに、どこで発生しているのか?さっぱり見当が付かない場合に二分法の考え方を応用します。
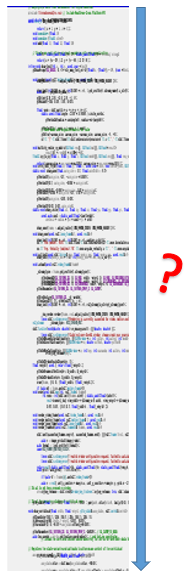
まず、エラーが発生しているプログラムにおいて、プログラムシーケンスのだいたい真ん中あたりとなる位置にブレークポイントを置いてデバック実行を行います。
もし、ブレークポイントまでエラーが無ければ、ブレークポイントの後半の処理でエラーが発生している事になります。
次に後半の処理部分のさらに真ん中あたりにブレークポイントを置き、デバッグ実行をしたときに、後半の中の前半の部分でエラーが発生していれば、エラーは全体の後半の中の前半部分で発生することがわかります。
これを繰り返すと、エラーが発生している位置は、全体の1/2⇒1/4⇒1/8・・・と追い込む事ができるので、やみくもにエラーの場所を探そうとするよりは、バグの位置を特定しやすくなるかと思います。
ラインセンサカメラで撮影した画像の縦横比を合わせる場合
ラインセンサカメラ(スキャナのような物)で撮影した画像は、何も考えずに撮影すると、縦横比が合わなく、丸い物を撮影しても楕円状になってしまいます。
これをまじめに縦横比を合わせるには、画像の横方向の撮影分解能(mm/画素)を画像から算出し、カメラのスキャンレート、エンコーダの撮影分解能、被写体の移動速度などから縦横比の合う値を算出します。
しかし、計算するのも少し面倒なので、ただ、撮影するだけの場合、私は画像を見ながら被写体の搬送速度を調整して縦横比を調整しています。
(実際の装置の場合、搬送速度は装置の生産能力に係わる部分なので、調整することは仕様的に難しい場合が多く、カメラのスキャンレートやエンコーダの撮影分解能などを調整して縦横比を合わせます。)
以下、具体例です。
送り方向に関しては、パルスモータで搬送しているとして、画像が縦長、横長になるパルス速度を見つけます。
(画像が縦長になるのは搬送速度が遅く、画像が横長になるのは搬送速度が速い事を意味します。)
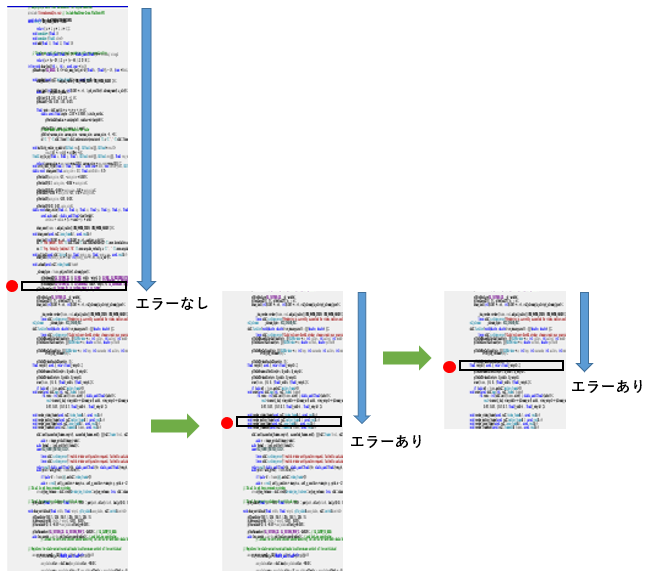
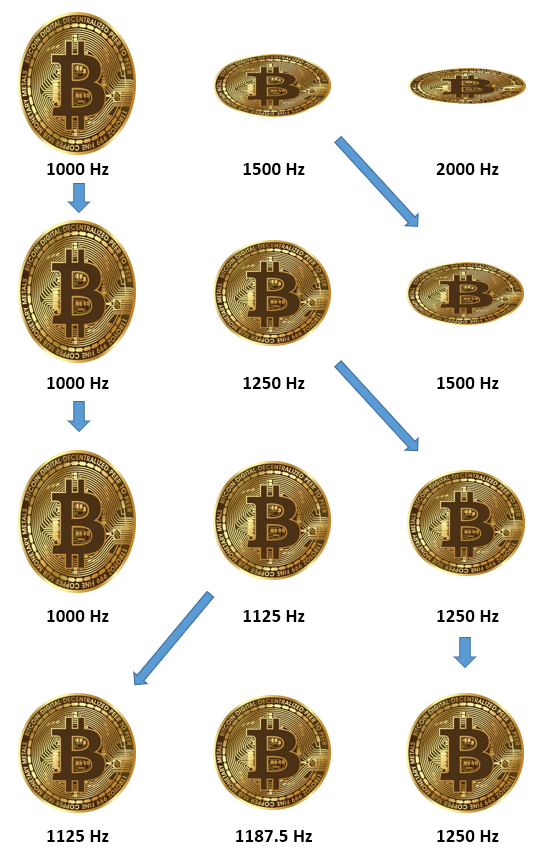
ここでは、パルス速度1000Hzで搬送した時に縦長、2000Hzで撮影した時に横長になったとすると、縦横比が合う搬送速度は1000~2000Hzの間にある事がわかります。
ここで、二分法の考え方を応用して、1500Hzで撮影した時に画像が横長になったとすると、縦横比が合う搬送速度は1000~1500Hzの間となります。
1250Hzで撮影した時に画像が横長になったとき、1000~1250Hzの間、
1125Hzで撮影した時に画像が縦長になったとき、1125~1250Hzの間、
1187.5Hzで撮影した時に・・・と繰り返していくと、縦横比の合う搬送速度を見つけ出す事ができます。
このように、二分法を知っていると、数式を解くだけでなく、効率的に目的の場所や値を求めることが出来るようになります。
←使える数学へ戻る



コメント