最小二乗法を用いて曲線近似するとき、近似するX座標の値が等間隔に並んでいる場合、奇関数、偶関数の特性を使って最小二乗法を高速に処理することが可能になります。
例えば、画像中の線の中心位置や、エッジの位置をサブピクセル単位で求める場合などに有効です。

以下からは線の輝度値を2次曲線で近似して、線の中心を求める例を示します。
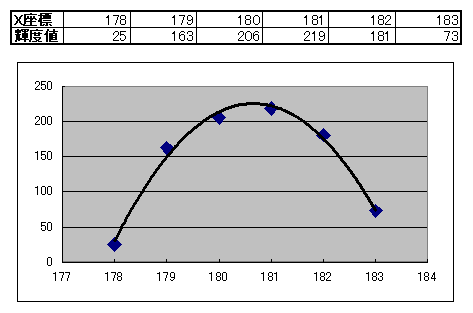
X方向の輝度値が最大となる座標付近の輝度値を抜き出し、2次式で近似すると
X座標が180と181との間に最大値がありそうな事が分かります。
この輝度値を二次式(Y = aX2 + bX + c)で近似する場合、下記の行列の式を解くと二次式が求まります。
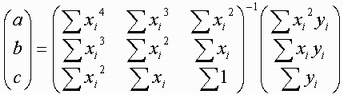
ここで、逆行列の中は奇関数、偶関数の集まりなので、輝度値データのX座標を中心座標(X = 180.5)で割り振ると
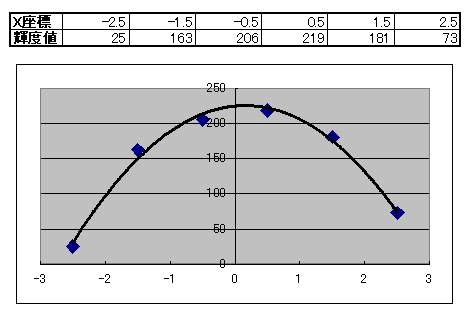
となります。
よって、奇関数、偶関数の特性から、行列の式は
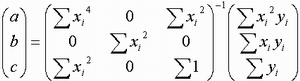
となり、行列の計算量を減らすことができます。
また、近似するデータの個数が固定できるなら、逆行列の部分はあらかじめ計算しておく事ができるので、さらに計算量を減らすことができます。
これで、求める線の中心座標は近似曲線の頂点位置、つまり微分の値が0となる座標(Y’ = 0の座標)なので、
線の中心座標 = Xの中心座標 – b / 2a
(今回の例ではXの中心座標 = 180.5)
となり、より高速に線の中心座標を求めることができるようになります。
この前提条件とした『X座標の値が等間隔に並んでいる場合』という部分ですが、画像処理においては、画素のX座標、Y座標を用いて、輝度値に関して近似する場合が多いので、for文などで、ある関数の総和などを求める場合には、この奇関数・偶関数が使えないか?検討してみると良いと思います。
このテクニックは計算量が格段に少なくなるので、効果的な場合が多いと思います。

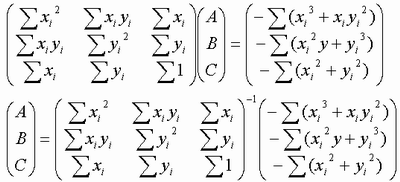
コメント