奇関数・偶関数の積分

奇関数・偶関数でも説明したように、

関数ｆ（ｘ）が奇関数の場合、-a～aの範囲での積分は

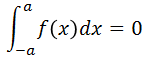
関数ｆ（ｘ）が偶関数の場合、-a～aの範囲での積分は

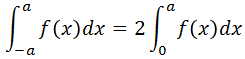
となります。

一般的な式では奇関数と偶関数に分けて積分を行います。

（計算例）

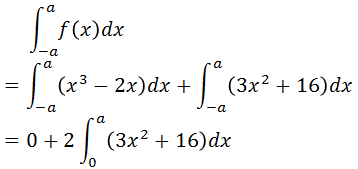
となります。

こうする事で計算量を格段に減らす事ができます。

現実的には積分の範囲が-a～aになる事はまれで、普通はa~bのような任意範囲で積分する場合が多いかと思います。

そこで、グラフ（関数）全体をaとbの中心[(a+b) / 2]が原点位置に来るように平行移動を行い、積分範囲が原点に対し対称になるように調整します。

（この処理を行っても積分の結果には影響はありません。）

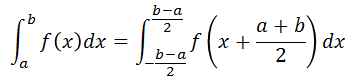
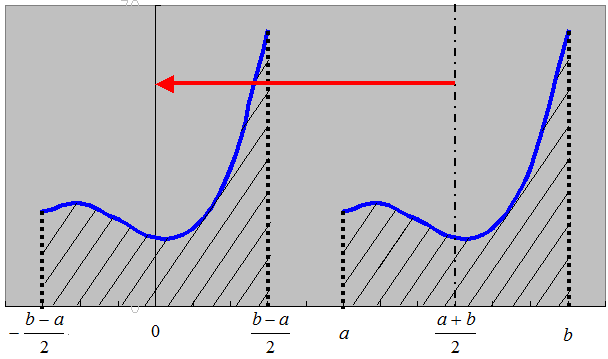
こうする事で、一般的な積分においても、奇関数・偶関数の特徴を用いる事が可能となります。

なぜ、わざわざそんな事をするかと言うと、積分の部分をfor文に置き換えて関数の合計を計算するプログラムを考えると、この奇関数・偶関数の特徴を用いると計算量が、

奇関数の部分で０へ

偶関数の部分で半分に

減らせる可能性があるので、トータルで1/4に計算量を減らせるかも？しれないので、その分、処理が高速になります。

その例を最小二乗法の最適化で紹介しています。