一般式による最小二乗法（円の最小二乗法）

ｎ次曲線による最小二乗法につていは説明しましたが、円や楕円、その他の一般式についても最小二乗法による近似は可能です。
今回は円の最小二乗法を例にとって説明しますが、他の一般式についても要領は同じです。

まず初めに近似する一般式を作成します。

円の場合、円の中心座標（a,b）、円の半径 r とすると

(X – a)² + (Y – b)² = r² ・・・①

となります。

ｎ次曲線による最小二乗法ではＸ座標がX_iの時のＹ座標Y_iと近似曲線上のＹ座標f(X_i)との差の二乗が最小になるように計算していましたが、円の場合、Ｘ座標がX_iの時にＹ座標が存在しなかったり、Ｙ座標が２点存在してしまう場合もあります。

そこで、今回はＹ座標の差の２乗の総和を求めるのではなく、①式を＝０の式に変形し、
点の座標(X_i,Y_i)を代入し、その式の２乗の総和を求めます。
（ｎ次式近似でやった計算も結局は近似式＝０になるように変形していた訳ですが．．．）

①式を＝０になるように変形し、２乗の総和は

∑｛(X_i – a)² + (Y_i – b)² – r²｝² = 0　・・・②

となります。

ただし、このまま未知数a,b,rに関して②式を偏微分してもa,b,rは４次関数となるので、各未知数の偏微分=0の時が最小とは限りません。

そこで、②式を展開し、下の式のように置きます。

∑｛X_i² + Y_i² + AX_i + BY_i + C｝² = 0　・・・③

ただし

A = -2a ・・・④
B = -2b ・・・⑤
C =  a² + b² – r² ・・・⑥

③式に関してＡ，Ｂ，Ｃについて偏微分すると

∂/∂A = A∑X_i² + B∑X_iY_i + C∑X_i + ∑X_i³ + ∑X_iY_i² = 0 ・・・⑦
∂/∂B = A∑X_iY_i + B∑Y_i² + C∑Y_i + ∑X_i²Y_i + ∑Y_i³ = 0 ・・・⑧
∂/∂C = A∑X_i + B∑Y_i + C∑1  + ∑X_i² + ∑Y_i² = 0 ・・・⑨

⑦、⑧、⑨式を行列を用いて解くと

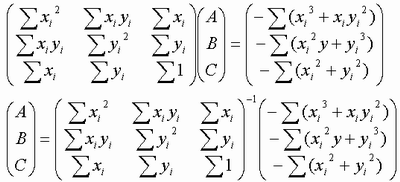
となり、逆行列を求めるとＡ，Ｂ，Ｃが求まります。

さらに④、⑤、⑥式より円の中心座標（a,b）、円の半径 rが求まります。

  \(a=-\frac{A}{2}\)

  \(b=-\frac{B}{2}\)

  \(r=\sqrt{a^{2}+b^{2}-C}\)

←使える数学へ戻る

関連記事

最小二乗法の計算方法

最小自乗法という人もいますが、私は最小二乗法派です。 最小二乗法とは？ 点の集まりから、近似直線（曲線）などの近似式を解くための手法です。 単に直線や二次曲線、三次曲線などに限らず、最小二乗法の応用範囲は広くあります。 最小二乗法は、言葉の...

imagingsolution.net

2011.06.02