複素数の計算

複素数については実在しないものの様に教わったので、なかなか理解できないままでいたのですが、実際に使ってみると便利に感じることもあるので、数学的には厳密でないかもしれませんが、私なりの理解でまとめてみます。

結論からすると、複素数は複素平面（横軸：実数、縦軸：虚数）におけるベクトルみたいなものです。ベクトルなので、大きさと角度を持ちます。
計算もベクトルと同じ様に、足し算、引き算ができます。
ただ、ベクトルと異なるのが、掛け算、割り算は、指数関数のように計算します。

 

まず、複素平面については、覚えるしか無さそうなので、複素数Zは実数成分がa、虚数成分がbのとき、虚数iを使って以下のように定義されます。

 

　複素数Z = a + bi

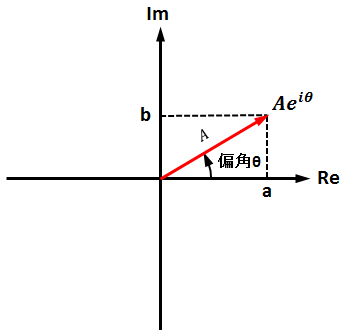
複素数の大きさ（絶対値は）

 

 

傾き（偏角）は

 

 

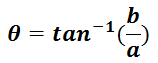
となります。

ここまでは、ほとんどベクトルもしくは極座標の計算と同じです。

 

さらに、オイラーの公式というのがあり、

e^iθ = cosθ + i sinθ

 

となります。

ここで登場するeはネイピア数と呼ばれるのですが、自然対数のeと同じフナ一羽二羽のe=2.718281828..と同じですが、指数のところに虚数のiが付いており、まじめにeの何乗か？と考えない方が良いかと思います。

 

e^iθは、複素平面上での半径１の円として捉えて下さい。

 

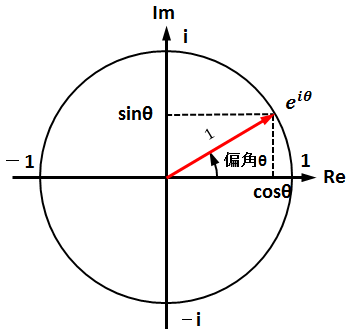
θ=0の時は

eⁱ⁰ = cos0 + i sin0　＝　１　＋　i 0 　= 　1

となり、θ=π / 2 のときは

e^iπ/2 = cos(π/2) + i sin(π/2)＝　0＋i 1 　= 　i

 

となります。

オイラーの公式では大きさが１ですが、最初の複素数の定義のように任意の大きさAとすると、合わせ技で

 

Ae^iθ = A(cosθ + i sinθ)  = a + bi

ただし、　a = Acosθ、 b = Asinθ

 

となります。

ここで大事なのが、複素数の定義ではベクトルのように見えますが、オイラーの公式を用いると指数関数のようにも見えます。

このどちらにも見える特性を都合のいい方で扱えるところが便利なところです。

 

例えば、２つの複素数Z₁とZ₂の足し算は

　　Z₁ = a₁ + b₁ i

　　Z₂ = a₂ + b₂ i

　　Z_１ + Z₂ = a₁ + b₁i + a₂ + b₂i  

　　　　　　= a₁ + a₂ + (b₁ + b₂)i

 

となります。

この計算は、ベクトル（a₁, b₁）とベクトル(a₂, b₂)の足し算と同じです。

 

 

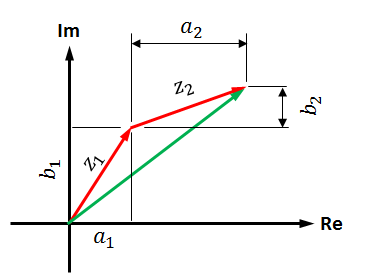
同様のことは引き算でも言えます。

 

それでは、掛け算の場合は、どうなるかというと

　　Z₁ = a₁ + b₁ i

　　Z₂ = a₂ + b₂ i

　　Z_１ x Z₂ = (a₁ + b₁i) x (a₂ + b₂i  )

　　　　　　= a₁a₂  +  a₁b₂ i + a₂b₁ i  + b₁b₂  i² 

　　　　　　= a₁a₂  + （a₁b₂  + a₂b₁ ）i  ー b₁b₂ 

　　　　　　= a₁a₂  ー b₁b₂ +（a₁b₂  + a₂b₁ ）i 

 

としてもいいのですが、オイラーの公式を使って、Z₁の絶対値をA₁,偏角をθ_１、Z_２の絶対値をA_２,偏角をθ_２として

 

　　Z₁ = a₁ + b₁ i　＝　A₁e^iθ１

　　Z₂ = a₂ + b₂ i　＝　A₂e^iθ2

　　Z_１ x Z₂ = A₁A₂ e^{i(θ１＋θ２)}

 

のように指数関数として複素数の掛け算（割り算）は計算した方が良い場合がよくあります。

 

 

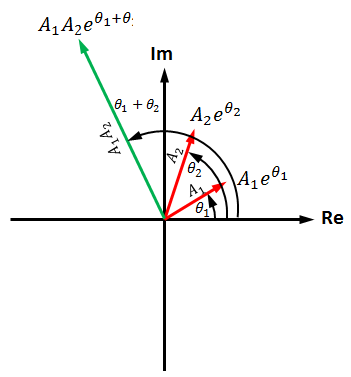
中間まとめ。

●複素数の足し算、引き算はベクトルの足し算、引き算

●複素数の掛け算、割り算は指数関数

 

と思って解ける場合が多い。

ここまで覚えると、複素数に関する公式は、覚えていなくても導き出せる場合が多いです。

 

例えば、虚数i は　i² = -1 となる値として教わったのですが、

$${ i }^{ 2 }={ \left( 0+1i \right) }^{ 2 }={ \left( { e }^{ i\frac { \pi }{ 2 } } \right) }^{ 2 }={ e }^{ i\left( \frac { \pi }{ 2 } +\frac { \pi }{ 2 } \right) }={ e }^{ i\pi }=-1$$

 

と考えると、回りくどいですが、自分の中ではスッキリと整理ができました。

 

他にも複素数の虚数成分を負にした（θをマイナスにした）ものを複素共役（ふくそきょうやく）といいますが、

$$Z\quad =\quad a\quad +\quad bi\quad =\quad A{ e }^{ i\theta }\quad \\ \bar { Z } \quad =\quad a\quad -\quad bi\quad =\quad A{ e }^{ -i\theta }\quad $$

 

図示するとこんな感じ↓

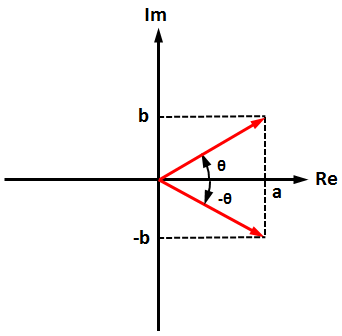
この特性から、実部aは複素共役を使うと

 

 

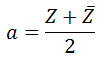
となりますが、図を見れば一目瞭然なので、あまり公式としては覚えていません。。

ただ、この複素共役ですが、分かりやすく　e^π/3 と　e^-π/3　のようにペアになってくれてればいいのですが、　e^π/3 と　e^5π/3　のような場合が多いので、ご注意下さい。

 

 

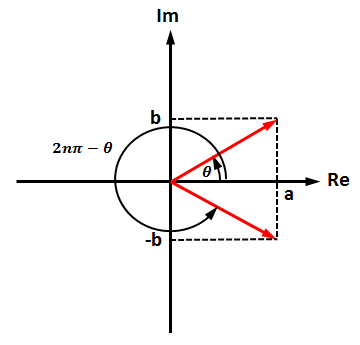
結局、この複素数を使うと何がよいか？というと、

●実数と虚数が同時に計算できる。普通の実数の空間で言うのなら、XとYが同時に計算できる。

●都合の良い方で計算できる。ベクトル演算だったり、指数関数だったり。。

●フーリエ変換的な要素（バンドパスフィルタ）が計算できる。

 

というのは、個人的な意見なのですが、実際にはプログラムを組む時は、実部と虚部で別々で計算していたりもします。

まぁ、画像処理アルゴリズムを考える時の手助けにはなっています。

 

←フーリエ変換、使える数学へ戻る